inf-schule | Softwarepatente: PageRank-Algorithmus

Zufallssurf-Modell

Bei dem bisherigen Zufallssurfer:innen-Modell aus dem letzten Abschnitt stellt man fest, dass sich nach einigen Zeitschritten alle Nutzer:innen beim Knoten D ansammeln.

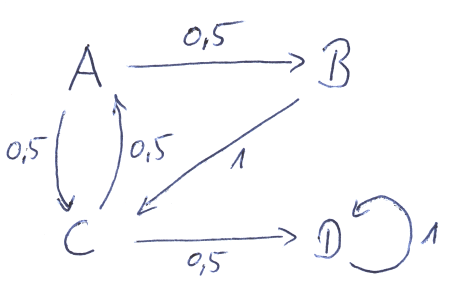
Daher erweitern wir unser bisheriges Modell um die Annahme, dass sich in jedem Zeitschritt jeweils 15% der Besucher:innen eines jeden Knotens gleichmäßig auf alle Knoten des Netzwerkes verteilen, indem sie zufällig irgendeine andere Webseite ansurfen. Die übrigen 85% verhalten sich wie in dem bisherigen Modell.

Die Gesamtzahl an Nutzer:innen, die in jedem Zeitschritt eine zufällige Webseite ansurfen beträgt: $$ 0,15 \, a_i + 0,15 \, b_i + 0,15 \, c_i + 0,15 \, d_i = 0,15 \, (a_i + b_i + c_i + d_i) = 0,15$$

Bezeichnen wir nun noch mit n die Anzahl der Knoten (in dem gewählten Beispiel also n=4), so erhalten wir folgendes iteratives Schema für die jeweiligen Zeitschritte:

$$\begin{array}{cccccccccc} a_{i+1} & = & 0,85 \; ( & & & & 0,5 c_i & & &) + 0,15 \frac{1}{n}\\ b_{i+1} & = & 0,85 \; ( & 0,5 a_i & & & & & &) + 0,15 \frac{1}{n}\\ c_{i+1} & = & 0,85 \; ( & 0,5 a_i & + & 1 b_i & & & &) + 0,15 \frac{1}{n} \\ d_{i+1} & = & 0,85 \; ( & & & & 0,5 c_i & + & 1 d_i &) + 0,15 \frac{1}{n} \end{array}$$ Wegen $a_i+b_i+c_i+d_i = 1$ können wir dies in Matrix-Vektor-Schreibweise ausdrücken als: $$\left(\begin{array}{c} a_{i+1}\\ b_{i+1}\\ c_{i+1}\\ d_{i+1} \end{array}\right) = 0,85 \left(\begin{array}{cccc} 0 & 0 & 0,5 & 0\\ 0,5 & 0 & 0 & 0\\ 0,5 & 1 & 0 & 0\\ 0 & 0 & 0,5 & 1 \end{array}\right) \left(\begin{array}{c} a_{i}\\ b_{i}\\ c_{i}\\ d_{i} \end{array}\right) + 0,15 \frac{1}{n} \left(\begin{array}{cccc} 1 & 1 & 1 & 1\\ 1 & 1 & 1 & 1\\ 1 & 1 & 1 & 1\\ 1 & 1 & 1 & 1 \end{array}\right) \left(\begin{array}{c} a_{i}\\ b_{i}\\ c_{i}\\ d_{i} \end{array}\right)$$ Nun führen wir noch die sogenannte Übergangsmatrix A und die Einsmatrix E und die Iterationsmatrix G wie folgt ein: $$A=\left(\begin{array}{cccc} 0 & 0 & 0,5 & 0\\ 0,5 & 0 & 0 & 0\\ 0,5 & 1 & 0 & 0\\ 0 & 0 & 0,5 & 1 \end{array}\right) \;\;\;\;\;\ E=\left(\begin{array}{cccc} 1 & 1 & 1 & 1\\ 1 & 1 & 1 & 1\\ 1 & 1 & 1 & 1\\ 1 & 1 & 1 & 1\\ \end{array}\right) \;\;\;\;\;\ \vec{v}_{i}=\left(\begin{array}{c} a_{i}\\ b_{i}\\ c_{i}\\ d_{i} \end{array}\right)$$ $$G := 0,85 A + \frac{1}{n}E =\left(\begin{array}{cccc} 0,0375 & 0,0357 & 0,4625 & 0,0375\\ 0,4625 & 0,0375 & 0,0375 & 0,0375\\ 0,4625 & 0,8875 & 0,0375 & 0,0375\\ 0,0375 & 0,0375 & 0,4625 & 0,0375\\ \end{array}\right)$$ Damit können wir das Iterationsschema in Kurzform schreiben als: $$ \begin{array}{ccl} \vec{v}{}_{i+1} &=& 0,85 A\vec{v}_{i} + \frac{1}{n}E \vec{v}_{i} \\ \vec{v}{}_{i+1} &=& ( 0,85 A + \frac{1}{n}E ) \vec{v}_{i} \\ \vec{v}{}_{i+1} &=& G \vec{v}_{i} \end{array} $$

Durchführen einiger Iterationsschritte liefert dann:

	i=0	i=1	i=2	...	i=20	i=30
a_i	0,25	0,1438	0,1889	...	0,1006	0,1006
b_i	0,25	0,1438	0,0986	...	0,0803	0,0803
c_i	0,25	0,3562	0,2208	...	0,1485	0,1485
d_i	0,25	0,3562	0,4917	...	0,6706	0,6707

Die Ergebnisse aus der Tabelle lassen vermuten, dass die prozentualen Anteile für gegen die folgenden feste Werte konvergieren: $$\begin{array}{cccc} a &:= lim_{i \rightarrow \infty} a_i = 0,1006\\ b &:= lim_{i \rightarrow \infty} b_i = 0,0803\\ c &:= lim_{i \rightarrow \infty} c_i = 0,1485\\ d &:= lim_{i \rightarrow \infty} d_i = 0,6707 \end{array}$$

Diese festen Grenzwerte nennt man PageRank-Werte der jeweils zugehörigen Webseiten. Sie geben ein Maß für die Wichtigkeit der betreffenden Webseiten an. In unserem Beispiel würden die Webseiten also durch die Suchmaschine in der folgenden Reihenfolge angezeigt werden:

D	wichtigste Webseite
C
A
B	unwichtigste Webseite

Anmerkung 1:

Der Vektor v=(a,b,c,d) wird durch G auf sich selbst abgebildet, also Gv = v. Ein solcher Vektor heißt Eigenvektor der Matrix G. Im Grundstudium der Mathematik, Informatik und der Physik beschäftigt man sich ausführlich mit den weiteren Eigenschaften solcher Eigenvektoren. Im Englischen wird übrigens der Fachbegriff eigenvector verwendet.

Anmerkung 2:

Tatsächlich gibt es einen Satz aus der Mathematik, mit dem sich beweisen lässt, dass das obige Schema unabhängig von der Größe des Graphen stets gegen feste Pagerank-Werte für die prozentualen Anteile an Webseitenbesuchern konvergiert. Der mathematische Satz heißt Theorem von Frobenius-Perron. Der Beweis dieses Satzes ist mit den Mitteln der Schulmathematik leider nicht leicht zugänglich und wird in der Schule daher nicht behandelt.