Das Rucksackproblem
Ein Rucksack voller Geschenke
Franziska ist die Gewinnerin bei der neuen Fernsehshow Knapsack
.
Als Gewinn erhält sie einen Rucksack, in den sie weitere Gegenstände aus einer vorgegebenen
Auswahl einpacken kann.
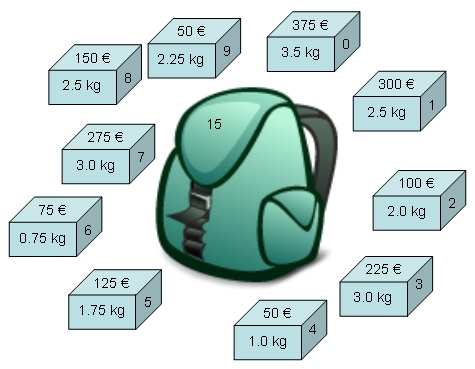
Es gibt allerdings einen kleinen Haken. Der Rucksack wird nach dem Einpacken der Gegenstände gewogen. Überschreitet das Gesamtgewicht die maximales Traglast von 15 kg, gibt es keinen Gewinn.
Aufgabe 1
Wie soll Franziska den Rucksack packen? Sie will einen möglichst großen Gewinn mitnehmen, ohne das Grenzgewicht zu überschreiten. Kannst du ihr bei der Lösung ihres Problem helfen?
Das Rucksackproblem
Das Rucksackproblem lässt sich allgemein wie folgt formulieren:
Gegeben sind n Gegenstände mit ihren Gewichten und Werten. Gegeben ist zusätzlich ein Grenzgewicht, das die maximale Traglast des Rucksacks beschreibt. Gesucht ist eine Kombination von Gegenenständen, so dass das Grenzgewicht nicht überschritten wird und der Gesamtwert der Gegenstände möglichst hoch ist.

Formal lässt das Rucksackproblem so formulieren:
Gegeben sind n Zahlenpaare (g0, w0), ..., (gn-1, wn-1) (die Gewicht und Wert von n Gegenständen beschreiben). Gegeben ist zusätzlich eine Grenzzahl G (die die maximale Traglast des Rucksacks beschreibt). Alle diese Zahlen sind beliebige (positive) Dezimalzahlen.
Gesucht ist eine 0-1-Folge x0, ..., xn-1 (die die Auswahl der Gegenstände beschreibt: 0 - nicht einpacken; 1 - einpacken), so dass x0*g0 + ... + xn-1*gn-1 <= G gilt und x0*w0 + ... + xn-1*wn-1 maximal ist.
Relevanz des Rucksackproblems
Das Rucksackproblem tritt immer dann auf, wenn ein Behälter
mit vorgegebener Kapazität
mit Gegenständen unterschiedlichen Wertes gefüllt werden soll. Dieser Fall tritt z.B. ein,
wenn ein LKW mit unterschiedlichen Gütern, die auch einen unterschiedlichen Gewinn erbringen,
beladen werden soll, dabei aber die maximale Ladelast nicht überschritten werden darf.

