NP-vollständige Probleme
Problemreduktion
Das Verfahren der Problemreduktion spielt eine entscheidende Rolle bei der Einordnung von Problemen in Komplexitätsklassen. Wir verdeutlichen es zuerst am Beispiel und betrachten das Hamilton-Problem und das Problem des Handlungsreisenden (in einer Entscheidungsvariante).
Beim Hamilton-Problem ist ein (ungerichteter und ungewichteter) Graph mit seinen Knoten und Kanten gegeben. Zu entscheiden ist, ob es einen Hamiltonkreis gibt - d.h. eine Rundreise durch den Graphen, in der jeder Knoten genau einmal vorkommt - nur Start- und Zielknoten kommen genau zweimal vor.
Beim Problem des Handlungsreisenden ist ein (ungerichteter und gewichteter, vollständiger) Graph mit seinen Knoten und gewichteten Kanten sowie eine Gewichtsschranke gegeben. Zu entscheiden ist, ob es eine Rundreise durch den Graphen gibt (in der jeder Knoten genau einmal vorkommt - nur Start- und Zielknoten kommen genau zweimal vor), so dass die Summe der Gewichte längs der Rundreise kleiner oder gleich der Gewichtsschranke ist.
Das Hamilton-Problem lässt sich auf das Problem des Handlungsreisenden zurückführen (reduzieren). Hierzu wird jedes konkrete Hamilton-Problem in ein entsprechendes Problem des Handlungsreisenden umgewandelt. Das folgende Beispiel soll die Umwandlung verdeutlichen.
Hamilton-Problem: Gibt es in Graph G einen Hamiltonkreis?
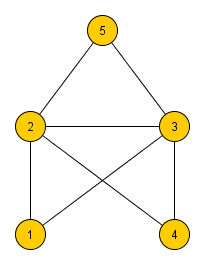
Zum ungewichteten Graphen G wird jetzt ein gewichteter Graph G' konstruiert,
indem die Knoten und Kanten von G übernommen werden, die Kanten von G mit dem Gewicht 1 bewertet und sämtliche noch
möglichen Kanten zwischen Knoten von G hinzugenommen und mit dem Gewicht 2 bewertet werden.
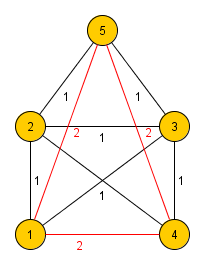
Problem des Handlungsreisenden: Gibt es in Graph G' eine Rundreise, dessen Gesamtgewicht
kleiner oder gleich der Anzahl der Knoten des Graphen ist?
Beachte, dass der Graph G' so konstruiert ist, dass ein Hamiltonkreis in G
einer Rundreise in G' mit dem Gesamtgewicht Anzahl der Knoten
entspricht.
Aus einem Algorithmus zur Lösung des Problem des Handlungsreisenden lässt sich jetzt direkt ein Algorithmus zur Lösung des Hamilton-Problem konstruieren.
Wir gehen davon aus,
dass ein Algorithmus existiertRundreiseHandlungsreisender existiert, der einen gewichteten Graphen und
eine Gewichtsschranke verarbeitet und entscheidet, ob es die gewünschte Rundreise gibt:
ALGORITHMUS existiertRundreiseHandlungsreisender
Übergabe: gewichteter Graph, Gewichtsschranke
# ...
Rückgabe: True / False
Hieraus entwickeln wir einen Algorithmus zur Lösung des Hamilton-Problems:
ALGORITHMUS existiertRundreiseHamilton
Übergabe: ungewichteter Graph G
# Umwandlung des Problems
erzeuge aus G den gewichteten Graphen G' (siehe oben)
gewichtsschranke = Anzahl der Knoten von G' (bzw. G)
# Lösung des transformierten Problems
ergebnis = existiertRundreiseHandlungsreisender(G', gewichtsschranke)
# Lösung des Ausgangsproblems
Rückgabe: ergebnis
Für den oben gegebenen Graphen G liefert existiertRundreiseHamilton(G)
das Ergebnis False, da existiertRundreiseHandlungsreisender(G', 5) das Ergebnis
False liefert.
Die folgende Abbildung verdeutlicht das Prinzip des Problemlösens durch Problemreduktion.
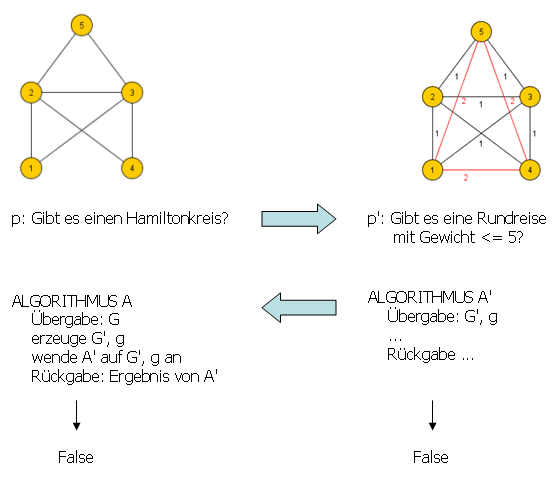
Polynomiale Problemreduktion
Bei einer polynomialen Problemreduktion muss der Aufwand zur Umwandlung des Problems (und zur Umwandlung der Lösung) polynomial sein.
Wir schreiben p ≤ p', wenn das Problem p auf das Problem p'
polynomial reduzierbar ist.
Beispiel: Das Hamilton-Problem ist auf das Problem des Handlungsreisenden polynomial reduzierbar. Die oben gezeigte Problemreduktion hat offensichtlich die geforderte Eigenschaft, dass die Problem- und Lösungsumwandlung mit polynomialem Aufwand erledigt werden kann. Übrigens: Man kann auch umgekehrt zeigen, dass das Problem des Handlungsreisenden auf das Hamilton-Problem polynomial reduzierbar ist.
Polynomiale Problemreduktionen werden bei Komplexitätsargumentationen benutzt. Die folgende Aussage soll gezeigt werden.
p ≤ p' und p' ∈ P ⇒ p ∈ P
In Worten: Wenn p auf das Problem p' polynomial reduzierbar ist
und wenn p' eine polynomiale Komplexität hat, dann hat auch das Problem p
eine polynomiale Komplexität.
Die Argumentation verläuft so: Aus einem Algorithmus A' mit polynomialer Komplexität zur
Lösung des Problems p' lässt sich ein Algorithmus A mit polynomialer Komplexität zur
Lösung des Problems p erzeugen. Man muss nur (wie im Beispiel oben) den Algorithmus
A' mit den Umwandlungsalgorithmen kombinieren. Bei der Argumentation benutzt man zudem,
dass das Hintereinanderausführen von Algorithmen mit polynomialer Komplexität zu einem
Algorithmus mit polynomialer Komplexität führt.
NP-vollständige Probleme
Ein Problem p* heißt NP-vollständig genau dann,
wenn es in der Komplexitätsklasse NP liegt
(d.h. mit einem nichtdeterministischen Algorithmus mit polynomialer Komplexität gelöst werden kann)
und wenn jedes Problem p aus NP auf p* polynomial reduzierbar ist.
NP-vollständige Probleme spielen bei der Klärung der Frage P=NP? eine zentrale Rolle.
Wenn es gelingt, ein NP-vollständiges Problem p* mit einem Algorithmus mit polynomialer Komplexität zu lösen,
dann ist die Aussage P=NP bewiesen. Denn, NP-Vollständigkeit bedeutet ja, dass jedes Problem
p ∈ NP auf p* polynomial reduzierbar ist. Aus einem polynomialen
Algorithmus für p* lässt sich dann ein polynomialer Algorithmus für jedes p ∈ NP
erzeugen.
Zur Klärung der Frage P=NP? konzentriert man sich also auf das Lösen NP-vollständiger
Probleme.
Es gibt inzwischen eine Vielzahl von Problemen, die als NP-vollständig nachgewiesen sind. Zu diesen Problemen gehören auch das Hamilton-Problem und das Problem des Handlungsreisenden.
Alle Versuche, ein NP-vollständiges Problem mit einem polynomialen Algorithmus zu lösen, sind
bisher fehlgeschlagen. Die NP-vollständigen Probleme erweisen sich also als harte Nüsse
und
gelten als schwer lösbare Probleme.
Aufgrund der vielen fehlgeschlagenen Versuche, einen polynomialen Lösungsalgorithmus für
ein NP-vollständiges Problem zu finden, vermutet man, dass die Frage P=NP?
negativ zu beantworten ist.

