Das Problem

Rundreise durch die Hauptstädte der Europäischen Union

Wenn ein neuer Außenminister im Amt ist, dann versucht er (oder sie), möglichst rasch Antrittsbesuche bei den wichtigsten Bündnispartnern zu machen. Zu diesen Partner gehören natürlich auch die Länder der Europäischen Union (EU).

Wir werden hier folgende Situation durchspielen: Nach einer Bundestagswahl soll der neue Außenminister alle Hauptstädte der EU besuchen. Die Reihenfolge soll sich nicht nach der Bedeutung der Länder oder anderen Kriterien richten. Sie soll so gewählt werden, dass der gesamte Reiseweg für den Minister möglichst gering wird.

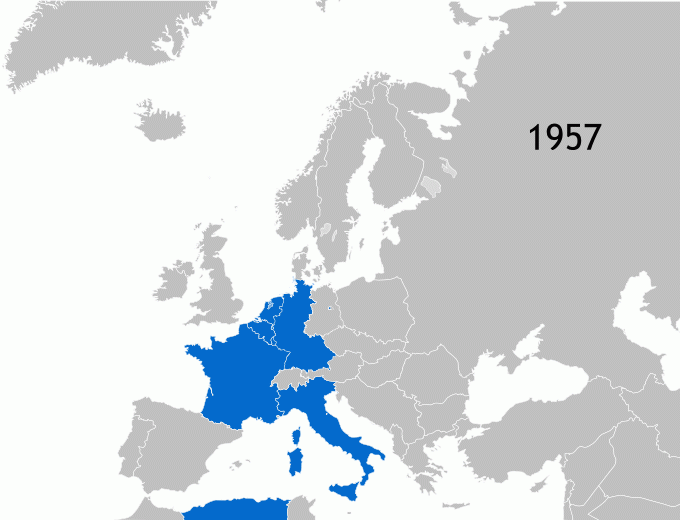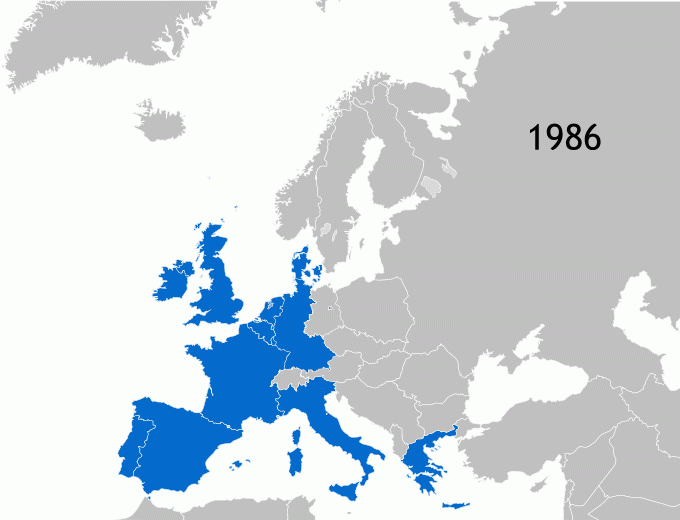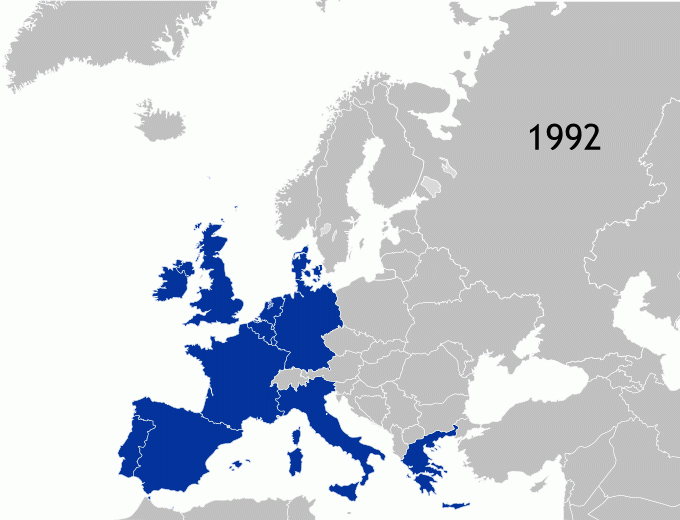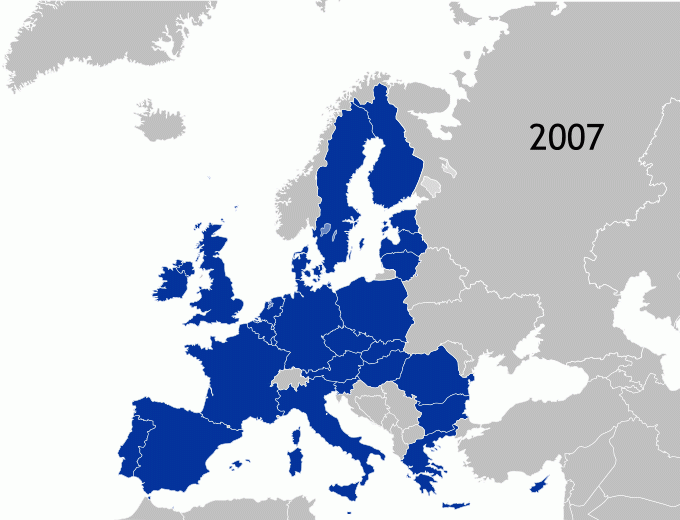
Bei der Bestimmung der kürzesten Rundreise durch die Hauptstädte der EU ist zu berücksichtigen, dass die EU einmal sehr klein - mit nur wenigen Bündnispartner - begonnen hat und dass im Laufe der Zeit immer mehr Mitgliedsstaaten hinzu gekommen sind. Die folgende Animation zeigt die Entwicklung der EU.

Aufgabe 1

Als Willy Brandt 1966 Außenminister wurde, bestand die EU (damals EWG) aus nur 6 Ländern: Deutschland, Frankreich, Italien, Niederlande, Belgien und Luxemburg. Die Tabelle zeigt die Entfernungen der jeweiligen Hauptstädte.

	Bonn	Paris	Rom	Den Haag	Brüssel	Luxemburg
Bonn	0	401	1066	244	195	145
Paris	401	0	1108	383	262	287
Rom	1066	1108	0	1289	1174	989
Den Haag	245	383	1289	0	137	302
Brüssel	195	262	1174	137	0	187
Luxemburg	145	287	989	302	187	0

Versuche, eine möglichst kurze Rundreise mit Start- und Zielort Bonn zu finden. Bestimme auch die Gesamtlänge der Rundreise.

Das Rundreiseproblem und seine Relevanz

Das Rundreiseproblem besteht darin, in einem gegebenen Graphen einen Kreis derart zu bestimmen, dass alle Knoten im Kreis vorkommen und die Länge des Kreises möglichst klein ist.

Weitere interessante Informationen und Anwendungen zum Rundreiseproblem findest du auf den Webseiten Traveling Salesman Problem.