Aufwandsanalyse
Fallanalysen
Bei einer Aufwandsanalyse unterscheidet man oft die folgenden Fälle:
- best case (bester Fall): der Fall, in dem bei der Ausführung des Algorithmus der geringste Aufwand erforderlich ist
- worst case (schlechtester Fall): der Fall, in dem bei der Ausführung des Algorithmus der meiste Aufwand erforderlich is
- average case (durchschnittlicher Fall): eine Mittelung über alle Fälle
Für die Praxis am wichtigsten ist meist der durchschnittliche Fall. Dieser ist aber schwer zu ermitteln. Wir konzentrieren uns hier daher auf den besten und schlechtesten Fall, wobei letzterer meist der relevantere ist.
Aufgabe 1
Betrachte eine lineare Suche in einer unsortierten bzw. sortierten Liste. Beschreibe jeweils den best case und den worst case. Gib auch an, wie viele Vergleiche man bei einer linearen Suche jeweils im best case und im worst case in einer Liste mit n Listenelementen benötigt.
Binäre Suche in einer sortierten Liste
Betrachte noch einmal die Vorgehensweise bei der binären Suche in einer sortierten Liste.
Fall 1: Das Datenobjekt kommt in der Liste vor.
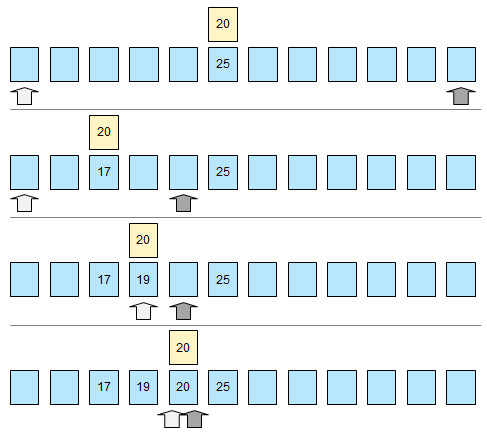
Fall 2: Das Datenobjekt kommt nicht in der Liste vor.
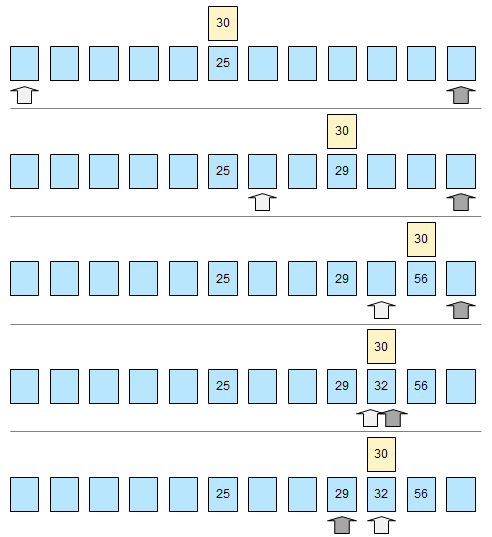
Aufgabe 2
(a) Begründe, dass man bei einer Listenlänge von n = 12 im worst case nur 4 Vergleiche benötigt, um das Suchproblem zu lösen.
(b) Ab welcher Listenlänge n benötigt man im worst case 3 bzw. 4 bzw. 5 bzw. 6 (bzw. k) Vergleiche? Entwickle eine Formel und teste mit der Animation (siehe unten).
(c) Ein Datenbestand bestehe aus ca. 1 Million Datensätzen. Wie viele Vergleiche benötigt man im worst case bei einer linearen Suche, falls der Datenbestand unsortiert ist? Wie viele Vergleiche benötigt man (in etwa) im worst case bei einer binären Suche, falls der Datenbestand sortiert ist? Erkläre mit den Ergebnissen, warum eine Vorsortierung eines Datenbestandes wichtig ist, wenn man sehr viele Suchvorgänge im Datenbestand durchführen muss.

