Station - Funktionen höherer Ordnung
Beispiel: Datensätze sortieren
Im Sportverein werden die Daten der Mitglieder mit einem Programm verwaltet. Für jedes Mitglied liegt ein Datensatz vor, der z.B. Vorname, Nachname, Geburtsdatum etc. enthält.
Programme zur Verwaltung solcher Daten bieten in der Regel eine Sortierfunktion an.
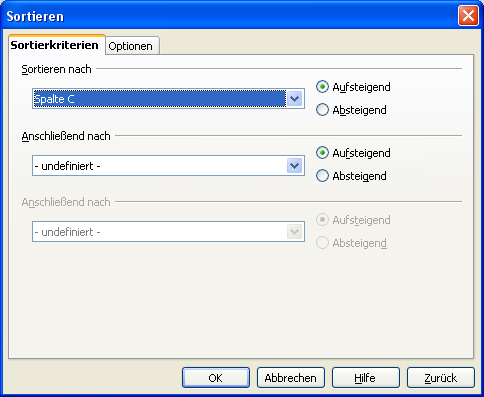
Mit Hilfe der Sortierfunktion können die Daten für bestimmte Zwecke umsortiert werden, z.B. nach Name und Vorname oder nach dem Geburtsdatum.
Es gibt eine Reihe von Sortierverfahren zur Realisierung der Sortierfunktion. Wir betrachten im Folgenden das Sortieren durch Einfügen (vgl. ...).
Ein erstes funktionales Programm
Eine funktionale Implementierung dieses Verfahrens könnte so aussehen:.
def einfuegen(e, L):
if len(L) == 0:
return [e]
else:
if e < L[0]:
return [e] + L
else:
return [L[0]] + einfuegen(e, L[1:])
def sortieren(L):
if len(L) == 0:
return L
else:
return einfuegen(L[0], sortieren(L[1:]))
Ziel ist es, die Funktion sortieren auf eine Liste mit Personendaten
anzuwenden.
personendaten = [
('Britta', 'Koch', (23,5,1995)),
('Paul', 'Schwarz', (11,11,2003)),
('Silke', 'Schmidt', (13,7,1990)),
('Jennifer', 'Abel', (15,12,1993)),
('Adriana', 'Müller', (21,1,2001)),
('Tobias', 'Klein', (1,3,1997)),
('Philipp', 'Bach', (21,4,1997)),
('Oliver', 'Schmitt', (14,4,1994)),
('Simone', 'Schuster', (20,12,2000)),
('Pia', 'Schwarz', (11,11,2003)),
('Andreas', 'Beyer', (16,3,1988)),
('Alexander', 'Heinrich', (17,3,1999)),
('Maximilian', 'Meyer', (21,6,1986))]
Die oben gezeigten Funktionsdefinitionen können noch nicht direkt auf die Liste mit den Personendaten angewandt werden, da die hier vorkommende Vergleichsoperation nicht für Tupel definiert ist. Wir müssen daher die Definitionen an geeigneter Stelle etwas modifizieren. Je nach Sortierkriterium erhalten wir dann leicht veränderte Funktionsdefinitionen:
Alphabetische Sortierung nach dem Nachnamen:
def einfuegen(e, L):
if len(L) == 0:
return [e]
else:
if e[1] < L[0][1]:
return [e] + L
else:
return [L[0]] + einfuegen(e, L[1:])
def sortieren(L):
if len(L) == 0:
return L
else:
return einfuegen(L[0], sortieren(L[1:]))
Alphabetische Sortierung nach dem Nach- und Vornamen:
def einfuegen(e, L):
if len(L) == 0:
return [e]
else:
if e[1] < L[0][1] or (e[1] == L[0][1] and e[0] < L[0][0]):
return [e] + L
else:
return [L[0]] + einfuegen(e, L[1:])
def sortieren(L):
if len(L) == 0:
return L
else:
return einfuegen(L[0], sortieren(L[1:]))
Aufgabe 1
Vergleiche die verschiedenen Funktionsdefinitionen. Worin unterscheiden sie sich? Teste sie durch Hinzufügen eines Testprogramms.
# Test
personendaten = [
('Britta', 'Koch', (23,5,1995)),
('Silke', 'Schmidt', (13,7,1990)),
('Jennifer', 'Abel', (15,12,1993)),
('Adriana', 'Müller', (21,1,2001)),
('Tobias', 'Klein', (1,3,1997)),
('Philipp', 'Bach', (21,4,1997)),
('Oliver', 'Schmitt', (14,4,1994)),
('Simone', 'Schuster', (20,12,2000)),
('Pia', 'Schwarz', (11,11,2003)),
('Andreas', 'Beyer', (16,3,1988)),
('Alexander', 'Heinrich', (17,3,1999)),
('Maximilian', 'Meyer', (21,6,1986)),
('Paul', 'Schwarz', (11,11,2003))]
print(sortieren(personendaten))
Aufgabe 2
Die Personendaten sollen nach dem Geburtsdatum (zuerst die/der Jüngste bzw. zuerst die/der Älteste) sortiert werden. Wie müssen die Funktionsdefinitionen abgeändert werden?
Ein verbessertes funktionales Programm
Es fällt auf, dass die Funktionsdefinitionen für die verschiedenen Sortierkriterien bis auf eine Bedingung identisch sind. Nur der Vergleich beim Einfügen muss an das jeweilge Sortierkriterium angepasst werden.
Es ist sicher keine gute Lösung, wenn man für die Funktionsdefinition für jedes Sortierkriterium neu anpassen muss. Geht das nicht auch einfacher? Die Antwort ist ja, wenn man eine Vergleichsrelation als Funktionsparameter zulässt.

Die Black-Box-Modellierungen zeigen Situationen, in denen eine Vergleichsoperation an die Funktion übergeben wird. In der oberen Abbildung wird als Vergleichsoperation der Vergleich der Nachnamen übergeben, in der unteren Abbildung ein Vergleich der Geburtsdaten.
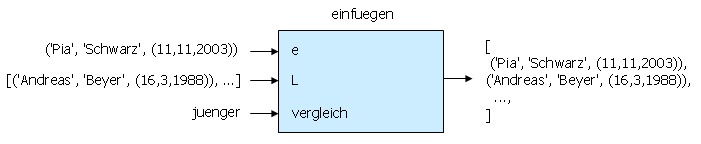
Funktionale Programmierung ermöglicht solche Situationen, in denen einer Funktion Daten übergeben werden können, die selbst eine Funktion darstellen.
Der folgende Quelltext zeigt, wie man die Übergabe einer Funktionen implementiert.
def einfuegen(e, L, vergleich):
if len(L) == 0:
return [e]
else:
if vergleich(e, L[0]) == True:
return [e] + L
else:
return [L[0]] + einfuegen(e, L[1:], vergleich)
def sortieren(L, vergleich):
if len(L) == 0:
return L
else:
return einfuegen(L[0], sortieren(L[1:], vergleich), vergleich)
Bei der Verwendung der Funktion muss jetzt die zu benutzende Vergleichsoperation als aktueller Parameter übergeben werden. Im foldenden Testprogramm werden zwei mögliche Verwendungen der funktion aufgezeigt.
# Test
personendaten = [
('Jennifer', 'Abel', (15,12,1993)),
('Philipp', 'Bach', (21,4,1997)),
('Andreas', 'Beyer', (16,3,1988)),
('Alexander', 'Heinrich', (17,3,1999)),
('Tobias', 'Klein', (1,3,1997)),
('Britta', 'Koch', (23,5,1995)),
('Maximilian', 'Meyer', (21,6,1986)),
('Adriana', 'Müller', (21,1,2001)),
('Silke', 'Schmidt', (13,7,1990)),
('Oliver', 'Schmitt', (14,4,1994)),
('Simone', 'Schuster', (20,12,2000)),
('Pia', 'Schwarz', (11,11,2003)),
('Paul', 'Schwarz', (11,11,2003))]
# Situation 1
def kleinerAlphabetischNachname(person1, person2):
if person1[1] < person2[1]:
return True
else:
return False
print(sortieren(personendaten, kleinerAlphabetischNachname))
# Situation 2
def geburtsdatum(person):
return person[2]
def tag(datum):
return datum[0]
def monat(datum):
return datum[1]
def jahr(datum):
return datum[2]
def kleinerDatum(datum1, datum2):
if jahr(datum1) < jahr(datum2) or \
jahr(datum1) == jahr(datum2) and monat(datum1) < monat(datum2) or \
jahr(datum1) == jahr(datum2) and monat(datum1) == monat(datum2) and tag(datum1) < tag(datum2):
return True
else:
return False
def juenger(person1, person2):
return kleinerDatum(geburtsdatum(person2), geburtsdatum(person1))
print(sortieren(personendaten, juenger))
Aufgabe 3
Teste die Funktionsdefinitionen. Sortiere die Personendaten auch nach Nach- und Vorname.
Funktionen höherer Ordnung
Eine Funktion höherer Ordnung ist eine Funktion, die Funktionen als Übergabedaten erhält oder eine Funktion als Rückgabedatum zurückliefert.
Ein einfaches Beispiel:
def rechnen(f, a, b):
return f(a, b)
def add(a, b):
return a + b
def sub(a, b):
return a - b
Die Funktion rechnen erwartet als ersten Parameter eine Rechenoperation, die mit Hilfe einer
Funktion dargestellt ist. Diese Rechenoperation wird dann auf die weiteren Parameter angewandt.
Die folgenden Funktionsaufrufe verdeutlichen das Verhalten der Funktion rechnen.
>>> rechnen(add, 3, 6)
9
>>> rechnen(sub, 5, 2)
3
Aufgabe 4
(a) Kann man die Funktion rechnen auch zur Ausführung von
Vergleichsoperationen benutzen? Führe hierzu geeignete Tests durch.
(b) Die Funktion anwenden ist folgendermaßen definiert:
def anwenden(f, a):
return f(a)
Teste die Funktion anwenden mit verschiedenen konkreten Funktionen.

