Station - Rekursion
Beispiel: Wie dreht man Wörter um?

Das Umdrehen von Wörtern soll jetzt mit einem Programm erledigt werden.
Iterativ zur Lösung
Die Grundidee einer iterativen Lösung besteht darin, ein neues Wort aufzubauen, indem Schritt für Schritt ein Zeichen im alten Wort entfernt und an die richtige Stelle im neuen Wort eingebaut wird. Das folgende Ablaufprotokoll verdeutlicht diesen Vorgang am Beispiel des Worts 'LEBEN'.
{neuesWort -> ''; altesWort -> 'LEBEN'}
neuesWort = altesWort[0] + neuesWort
altesWort = altesWort[1:]
{neuesWort -> 'L'; altesWort -> 'EBEN'}
neuesWort = altesWort[0] + neuesWort
altesWort = altesWort[1:]
{neuesWort -> 'EL'; altesWort -> 'BEN'}
neuesWort = altesWort[0] + neuesWort
altesWort = altesWort[1:]
{neuesWort -> 'BEL'; altesWort -> 'EN'}
neuesWort = altesWort[0] + neuesWort
altesWort = altesWort[1:]
{neuesWort -> 'EBEL'; altesWort -> 'N'}
neuesWort = altesWort[0] + neuesWort
altesWort = altesWort[1:]
{neuesWort -> 'NEBEL'; altesWort -> ''}
Zur Verwaltung des neuen wie auch des alten Worts werden hier neue Variablen eingeführt. Mit Hilfe von Zuweisungen werden die Werte der Variablen schrittweise verändert. Der gesamte Ablauf lässt mit der Kontrollstruktur "Wiederholung" wie folgt modellieren:
Eingabe: wort
altesWort = wort
neuesWort = ''
SOLANGE altesWort noch Zeichen enthält:
füge das erste Zeichen von altesWort vorne in neuesWort ein
entferne das erste Zeichen von altesWort
Ausgabe: neuesWort
Dieses Ablaufmodell lässt sich mit einer imperativ definierten Funktion implementieren.
# Eingabe
wort = input('Wort: ')
# Verarbeitung
altesWort = wort
neuesWort = ''
while len(altesWort) > 0:
neuesWort = altesWort[0] + neuesWort
altesWort = altesWort[1:]
# Ausgabe
print(neuesWort)
Rekursiver Ansatz
Wenn man auf Zuweisungen an Variablen verzichten will, benötigt man eine neue Idee zur Problemlösung. Diese besteht hier darin, das Problem schrittweise in ein strukturgleiches Problem zu reduzieren. Die folgende Reduktionskette verdeutlicht diesen Vorgang am Beispiel des Worts 'LEBEN'.
umdrehen('LEBEN') ->
(umdrehen('EBEN') + 'L') ->
((umdrehen('BEN') + 'E') + 'L') ->
(((umdrehen('EN') + 'B') + 'E') + 'L') ->
((((umdrehen('N') + 'E') + 'B') + 'E') + 'L') ->
(((((umdrehen('') + 'N') + 'E') + 'B') + 'E') + 'L') ->
((((('' + 'N') + 'E') + 'B') + 'E') + 'L') ->
(((('N' + 'E') + 'B') + 'E') + 'L') ->
((('NE' + 'B') + 'E') + 'L') ->
(('NEB' + 'E') + 'L') ->
('NEBE' + 'L') ->
'NEBEL'
Beachte, dass hier keine Variablen eingeführt werden.
Es werden zwei Sorten von Problemreduktionsschritte ausgeführt. Zum einen werden Schritte ausgeführt, die das Problem auf eines in verkleinerter Form reduzieren. Beachte, dass der Wert des Terms sich bei einer solchen Problemreduktion nicht verändert.
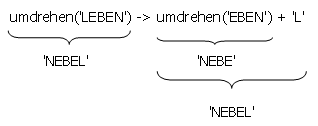
Zum anderen wird ein Schritt ausgeführt, der schließlich das (kleinstmögliche) Problem direkt löst.
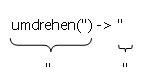
Die Problemreduktionsschritte lassen sich verallgemeinernd durch Reduktionsregeln beschreiben:
Fall 1: wort == '' umdrehen(wort) -> wort Fall 2: wort != '' umdrehen(wort) -> umdrehen(wort[1:]) + wort[0]
Dieses Reduktionsregelmodell lässt sich mit einer rekursiv definierten Funktion implementieren.
def umdrehen(wort):
if len(wort) == 0:
return wort
else:
return umdrehen(wort[1:]) + wort[0]
Mit einem Funktionsaufruf erhält man die Lösung zu einem vorgegebenen konkreten Problem.
>>> umdrehen('LEBEN')
'NEBEL'
Was ist eigentlich eine rekursive Problemreduktion?
 Rekursive Problemreduktion ist eine Problemlösestrategie, bei der ein Problem
auf ein strukturgleiches Problem (in
Rekursive Problemreduktion ist eine Problemlösestrategie, bei der ein Problem
auf ein strukturgleiches Problem (in verkleinerter
Form) zurückgeführt wird.
Hier ein Beispiel:
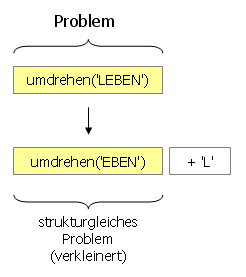
Das Problem "Umdrehen der Zeichenkette 'LEBEN'" können wir auf das
entsprechende Problem "Umdrehen der Zeichenkette 'EBEN'" zurückführen.
Rekursive Funktionsdefinitionen
Eine rekursive Funktionsdefinition ist eine Funktionsdefinition, bei der die Funktion selbst im Funktionsterm benutzt wird.
Beispiel einer rekursiven Funktionsdefinition:
def umdrehen(wort):
if len(wort) == 0:
return wort
else:
return umdrehen(wort[1:]) + wort[0]
Bei der Auswertung von Funktionsaufrufen kommt es bei rekursiven Funktionsdefinitionen zur wiederholten Ausführung strukturgleicher Reduktionsschritte. Rekursion kann somit als Ersatz für die Kontrollstruktur "Wiederholung" benutzt werden.
Damit dieses Wiederholungskonzept terminiert, muss nach endlichen vielen Reduktionsschritten eine Situation (der sog. Rekursionsanfang) erreicht werden, bei der die Lösung zum Problem direkt angegeben werden kann.
Man versucht daher, Reduktionsschritte so zu konzipieren, dass sie das Problem in einer Weise "verkleinern", die nur endlich viele Verkleinerungsschritte zulässt. Im oben gezeigte Beispiel besteht die Verkleinerung darin, die Länge der Zeichenkette um 1 zu reduzieren. Nach endlich vielen Reduktionsschritten kommt man so sicher zur leeren Zeichenkette.
Rekursion ist eine mächtige und gerne genutzte Strategie beim Problemlösen. Wenn der Problemkontext es zulässt, dann kann man das Problemlöseverfahren sehr einfach und kompakt über eine Problemreduktion beschreiben. Die wiederholte Ausführung der Reduktionsschritte - und damit die Erzeugung der eigentlichen Lösung - überlässt man dem Ausführsystem.
Aufgabe 1
Führe die folgende Funktion mit geeigneten Funktionsaufrufen aus und erkläre die produzierten Ausgaben.
def umdrehen(wort):
print('Uebergabe:', wort)
if len(wort) == 0:
ergebnis = wort
else:
ergebnis = umdrehen(wort[1:]) + wort[0]
print('Rueckgabe:', ergebnis)
return ergebnis
Aufgabe 2
Noch eine rekursive Funktionsdefinition! Kannst du vorhersagen, welche Ausgaben bei der Auswertung
des Funktionsaufrufs verarbeiten('TOR') hier gemacht werden? Überprüfe deine Vermutung.
def verarbeiten(wort):
print('Uebergabe:', wort)
if len(wort) == 0:
ergebnis = wort
else:
ergebnis = wort[0] + wort[0] + verarbeiten(wort[1:])
print('Rueckgabe:', ergebnis)
return ergebnis

