Geheimnisteilen
Eine geometrische Variante des Geheimnisteilens – Aufgaben
Theorie
- Bestimme aus den beiden Teilgeheimnissen G1 = ( 1,8 ) und G2 = ( 2,4 ) Schritt für Schritt wieder das Geheimnis G.
- Konstruiere selbst als Geheimnishüterin zum Geheimnis G = 8 zwei Teilgeheimnisse mit der geometrischen Methode.
- Lese aus dem folgenden Bild das Geheimnis
G sowie zwei Teilgeheimnisse G1 und G2 ab:
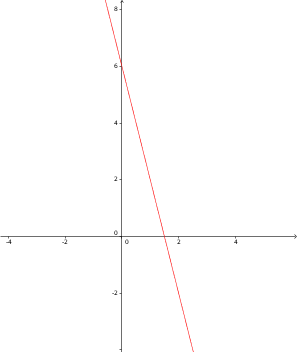
- Prüfe anschließend die Richtigkeit deiner Ableseergebnisse, indem du aus den beiden abgelesenen Teilgeheimnissen G1 und G2 das Geheimnis G berechnest.
- Lese aus dem folgenden Bild das Geheimnis
Implementierung und Ausblick
- Entwickle und implementiere ein Programm in Python, dass bei Angabe zweier Teilgeheimnisse das Geheimnis ausgibt.
- Überlege dir und prüfe anschließend, ob die Eingabe zu deinem Programm, die zu der Ausgabe des Geheimnisses führt eindeutig ist.
- Kann ein Geheimnis mit dieser geometrischen Methode auch auf drei, vier, oder fünf Personen aufgeteilt werden, sodass alle Geheimnisträger ein verschiedenes und zur Bestimmung des Geheimnisses notwendiges Teilgeheimnis besitzen?

