Station - Korrektheit und Sicherheit
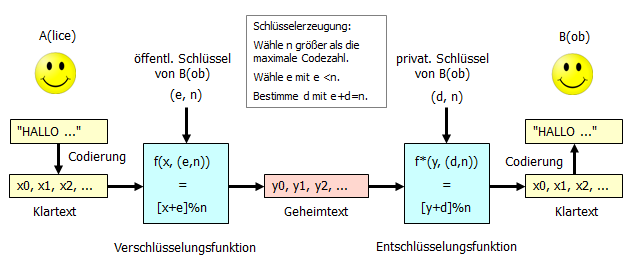
Das Verfahren mit modularer Addition
Korrektheit des Verfahrens mit modularer Addition
Korrektheit bedeutet hier, dass das Entschlüsseln das Verschlüsseln wieder rückgängig macht.
Die Korrektheit des beschriebenen Verfahrens ist leicht einzusehen. Wir betrachten eine Codezahl x, die mit dem öffentlichen Schlüssel (e, n) verschlüsselt und anschließend mit dem privaten Schlüssel (d, n) entschlüsselt wird.
x
↓ # verschlüsseln
[x + e]%n
↓ # entschlüsseln
[[x + e]%n + d]%n
= [x + [e + d]%n]% n # Rechengesetze
= [x + 0]%n # Schlüsseleigenschaft
= [x]%n # Rechengesetz
= x # Schlüsseleigenschaft
Damit ist also gezeigt, dass das Verfahren korrekt ist, weil die Entschlüsselung das Verschlüsseln wieder rückgängig macht.
Neben Rechengesetzen haben wir hier die Eigenschaft der beiden Schlüssel ausgenutzt. Nämlich die Eigenschaft, dass die beiden Schlüssel e und d invers zueinander bzgl. der Modulzahl sind: e + d = n bzw. [e + d]%n = 0.
Sicherheit des Verfahrens mit modularer Addition
Das Verfahren mit modularer Addition ist völlig unsicher.
Aus dem öffentlichen Schüssel (e, n) kann man direkt den privaten Schlüssel (d, n) berechnen. Es gilt d = n - e.
Wenn man das Verschlüsselungsverfahren und den öffentlichen Schlüssel kennt, dann ist man direkt in der Lage, den privaten Schlüssel zu bestimmen und verschlüsselte Texte wieder zu entschlüsseln.
Aufgabe 1
Der Quelltext wurde mit unserem Codierverfahren in Zahlen umgewandelt. Dabei wurde eine Blocklänge 2 benutzt.
Der öffentliche Schlüssel ist (3210, 4711).
Mit diesem öffentlichen Schlüssel wurde der Geheimcode [3322, 4415, 399, 4322, 3328] erzeugt. Kannst du den Geheimcode entschlüsseln?

