Von der Grammatik zum Automaten
Verarbeitung einer Grammatik für Binärzahlen
Die Sprache LBin = {0, 1, 10, 11, 100, 101, 110, 111, 1000, ...}
der Binärzahlen kann man mit einer Reihe von Grammatiken beschreiben, u.a. mit der folgenden: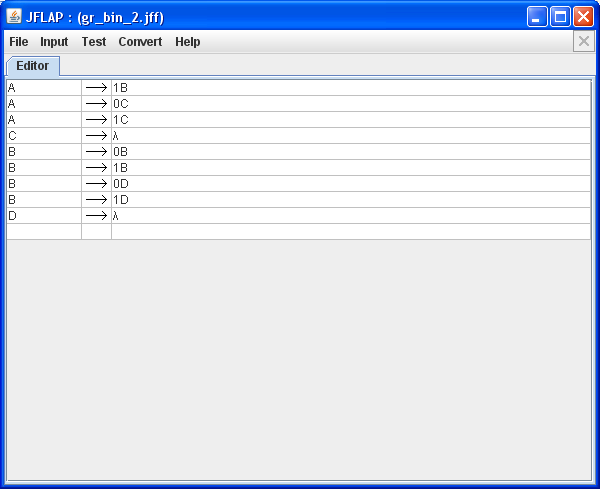
Nach Eingabe der Grammatik bietet JFlap die Menupunkte [Convert][Convert Right-Linear Grammar to FA] an. Jetzt kann man einzelne Produktionen auswählen und sich die entsprechenden Zustandsübergänge im Automaten erzeugen lassen.
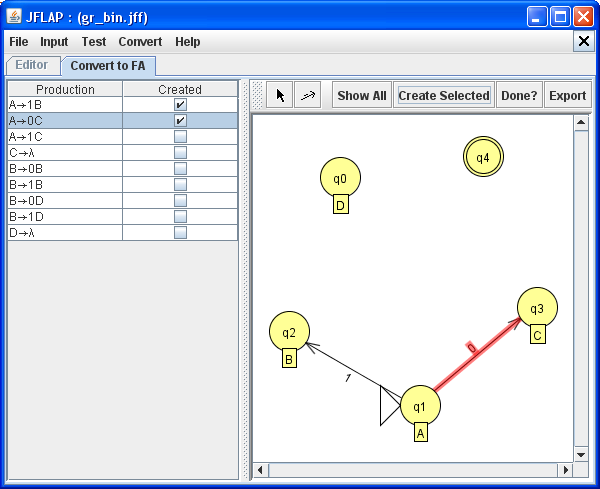
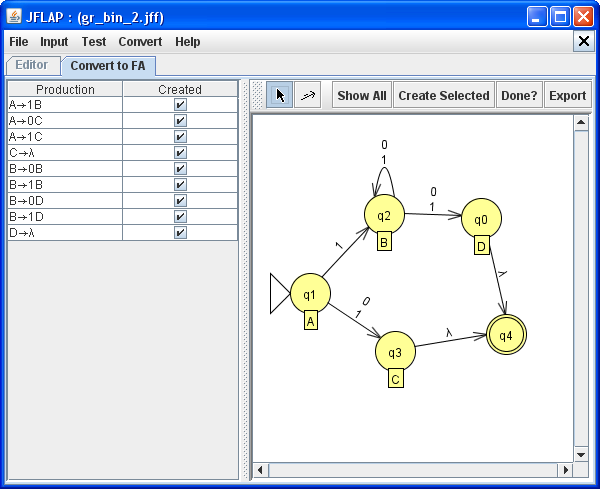
Wenn alle Produktionen verarbeitet sind, erhält man folgenden Automaten:
Aufgabe 1
Probiere das selbst einmal aus. Wie wird der Automat zur Grammatik erzeugt?
Aufgabe 2
Der resultierende Automat ist kein endlicher Automat im bisherigen Sinne. Welche Besonderheiten fallen auf?

