Fachkonzept - Typdefinition
Grundidee
Zu verarbeitende Daten können von ganz unterschiedlichem Typ sein: z.B. Zahlen oder Zeichenketten oder Listen mit Datensätzen.
Zur Modellierung all dieser verschiedenen Daten stellt Elm vordefinierte Datentypen wie Int, String oder List a
zur Verfügung.
Manchmal gibt es Situationen, in denen eine Datenmodellierung mit den von Elm vorgegebenen Datentypen die Datenwelt nicht gut widergibt. Betrachte als Beispiel eine Situation, in der man die 4 Himmelsrichtungen als Daten benutzen möchte. Eine Datenmodellierung mit Zeichenketten ist hier durchaus möglich.
drehen: String -> String
drehen richtung =
case richtung of
"Norden" -> "Osten"
"Osten" -> "Süden"
"Süden" -> "Westen"
"Westen" -> "Norden"
Es gibt aber Schwierigkeiten bei der Verarbeitung.
-- MISSING PATTERNS -------------------------------------- src\Main.elm
This `case` does not have branches for all possibilities:
6|> case richtung of
7|> "Norden" -> "Osten"
8|> "Osten" -> "Süden"
9|> "Süden" -> "Westen"
10|> "Westen" -> "Norden"
Missing possibilities include:
_
I would have to crash if I saw one of those. Add branches for them!
Bei Funktionen vom Typ String -> String muss man immer für alle möglichen String-Werte die Rückgabe festlegen, hier z.B. so:
drehen: String -> String
drehen richtung =
case richtung of
"Norden" -> "Osten"
"Osten" -> "Süden"
"Süden" -> "Westen"
"Westen" -> "Norden"
_ -> "?"
Die Funtion drehen ist also nicht mehr nur für Himmelsrichtungen definiert.
Wenn man tatsächlich nur die 4 Himmelsrichtungen verarbeiten möchte, dann braucht man einen Datentyp, der nur genau 4 Datenwerte - für die betreffenden Richtungen - hat. Einen solchen Datentyp muss man dann selbst definieren.
Definition eines Datentyps
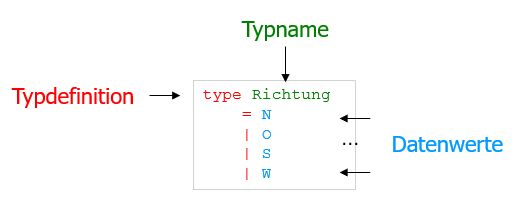
Eine Typdefinition erzeugt einen Datentyp, indem ein Typname mit einer Beschreibung der zugehörigen Datenwerte verknüpft wird.
Die Abbildung verdeutlicht eine solche Typdefinition für Himmelsrichtungen. Hier werden die Bezeichner für die Datenwerte (hier: N, O, S, W) über eine Fallunterscheidung aufgelistet.
Die Verarbeitung der neu definierten Daten erfolgt in der Regel mit einem case-Ausdruck.
Hier ein Beispiel.
type Richtung
= N
| O
| S
| W
drehen: Richtung -> Richtung
drehen richtung =
case richtung of
N -> O
O -> S
S -> W
W -> N
umwandlung: Richtung -> String
umwandlung richtung =
case richtung of
N -> "Norden"
O -> "Osten"
S -> "Süden"
W -> "Westen"
> drehen N
O : Richtung
> umwandlung O
"Osten" : String
Definition komplexer Datentypen
Als Beispiel betrachten wir die Definition eines Datentyps für Bewegungsbefehle.
type Befehl
= LI -- links
| RE -- rechts
| VW Int -- vorwärts ...
| WH Int (List Befehl) -- wiederhole ...
Der folgende REPL-Dialog verdeutlicht, dass mit dieser Typdefinition komplexe Daten erzeugt werden.
> LI
LI : Befehl
> VW 3
VW 3 : Befehl
> WH 4 [VW 1, RE]
WH 4 [VW 1,RE] : Befehl
> WH 2 [VW 3, WH 4 [VW 1, RE]]
WH 2 [VW 3,WH 4 [VW 1,RE]]
: Befehl
Beachte, dass Daten wie VW 3 zusätzliche Werte umfassen können.
Beachte auch, dass die rekursive Typdefinition geschachtelte Daten wie z.B. WH 2 [VW 3, WH 4 [VW 1, RE]] ermöglicht.
Die Verarbeitung solch komplexer Daten ist dann entsprechend komplex.
type Befehl
= LI -- links
| RE -- rechts
| VW Int -- vorwärts ...
| WH Int (List Befehl) -- wiederhole ...
weglaenge befehl =
case befehl of
LI -> 0
RE -> 0
VW x -> x
WH n befehle -> n * (List.map weglaenge befehle |> List.foldr (+) 0)
> weglaenge (WH 2 [VW 3, WH 4 [VW 1, RE]])
14 : Int
Quellen
- [1]: Typdefinition - Urheber: KB - Lizenz: inf-schule.de