Einordnung
Beim Suchen der Datei "Lösungen_Klassenarbeit_Informatik.pdf" hast du wahrscheinlich eine rekursive Strategie entwickelt, die sich immer wiederholt hat: Ordner öffnen, Inhalt prüfen. Wenn ein Unterordner auftaucht, wendest du genau dieselbe Suchstrategie auf diesen neuen, "kleineren" Suchbereich (den Unterordner) an. Du hast also das Prinzip der Rekursion angewendet, indem du das Problem auf eine kleinere Version seiner selbst zurückgeführt hast.
Das Schema der rekursiven Problemlösung
Die Strategie, ein Problem zu lösen, indem man es auf eine kleinere Version seiner selbst zurückführt, bis man bei einem einfachen, direkt lösbaren Fall ankommt, nennen wir rekursive Problemlösung. Das hast du auch im ersten Kapitel schon gelernt. Jetzt wollen wir diese Strategie nochmal etwas abstrakter darstellen.
Wenn wir ein Problem haben, welches wir nicht direkt lösen können, z.B. "Ist 'Lösungen_Klassenarbeit_Informatik.pdf' irgendwo im riesigen Ordner 'Dokumente'?", können wir das Problem reduzieren (Rekursionsschritt): "Öffne 'Dokumente'. Ah, ein Unterordner 'Bilder'! Jetzt lautet das Problem: Ist die Datei irgendwo im Unterordner 'Bilder'?". Wenn wir ein Problem versuchen direkt zu lösen, sagen wir dazu ad-hoc (quasi "spontan"). Das kleinere Problem gehen wir mit derselben Logik an. Die Lösung dieses kleineren Problems erweitern wir dann zu der Lösung des ursprünlgichen Problems. Im Fall des Dateisuchens, bei dem die Lösung des Problems einfach ein schlichtes "Ja" oder "Nein" ist, ist das noch relativ simpel. Wenn wir an die Probleme aus dem ersten Kapitel denken, wie beispielswiese die Fakultät, dann müssen wir mit dem Ergebnis des rekursiven Aufrufs bzw. des kleineren Problems noch etwas tun, um auf die Lösung des ursprünglichen Problems zu kommen. Das Diagramm im Folgenden soll das alles nochmal visualisieren.
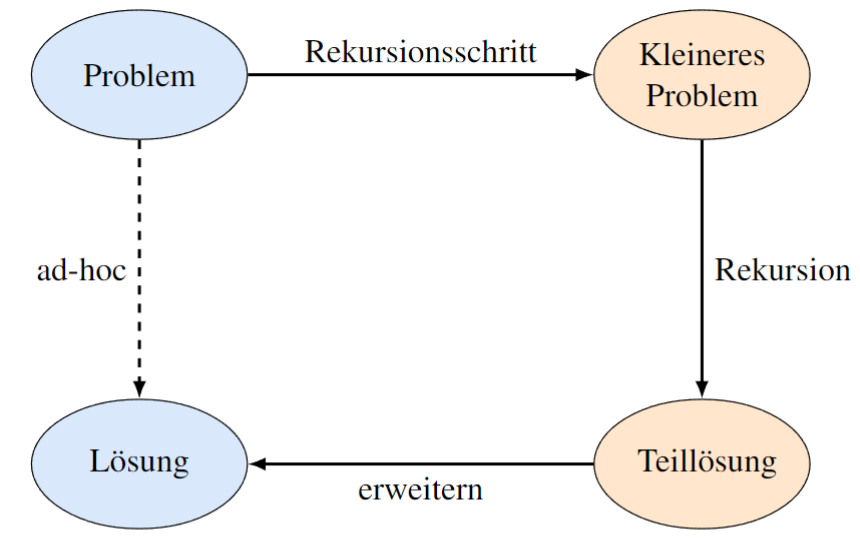
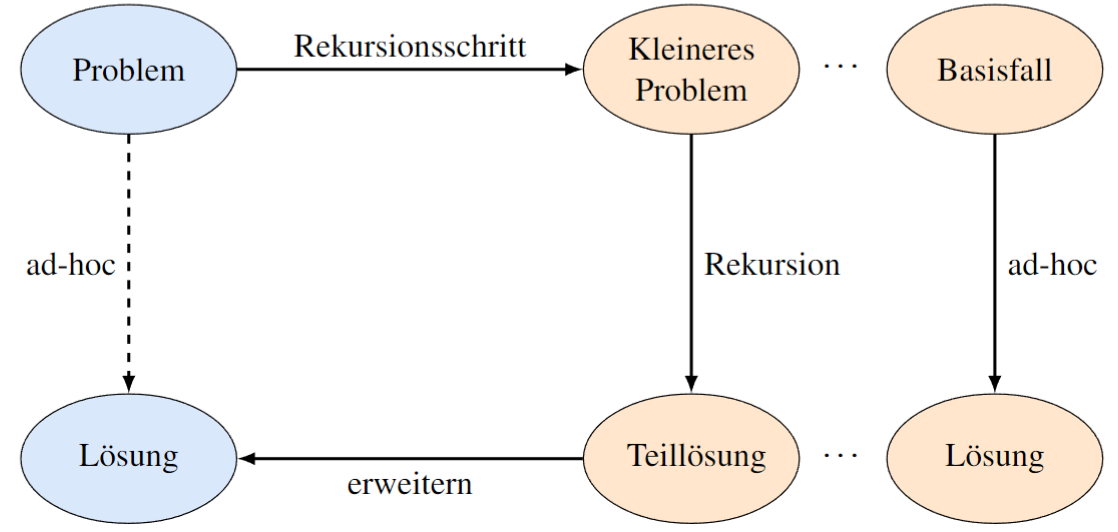
Dieses Zerlegen in immer kleinere, gleichartige bzw. strukturgleiche Probleme geschieht so lange, bis wir auf den Basisfall stoßen – das Problem, das so klein ist, dass wir es direkt, also ad-hoc, lösen können. In unserem Beispiel wäre entweder die Datei im aktuell betrachteten Ordner, oder der aktuell betrachtete Ordner enthält keine weiteren Unterordner und die Datei ist auch nicht unter den direkten Dateien. Diese Lösung wird dann an die nächstgrößere Instanz weitergegeben, die damit dann weiter arbeitet bzw. weiter rechnet.
Aufgabe 2
Wir betrachten die Funktion reverse(liste), die versucht, eine Liste rekursiv umzukehren ("reverse" ist englisch für umkehren). Schau dir zunächst ein paar Beispielausgaben an.
>>> reverse([1, 2, 3, 4, 5])
[5, 4, 3, 2, 1]
>>> reverse([4711])
[4711]
>>> reverse(['a', 'b', 'c'])
['c', 'b', 'a']
>>> reverse([True, False, False])
[False, False, True]
- Beantworte zunächst die folgenden Fragen:
- Was ist die kleinste Instanz des Problems und was sollte die Funktion in diesem Fall zurückgeben?
- Wie kann man das Problem im rekursiven Schritt verkleinern?
- Wie wird das Ergebnis des rekursiven Aufrufs verwendet, um das Endergebnis zu erzeugen?
- Die Aufrufe oben sind mit verschiedenen Arten von Listen gemacht. Nenne Unterschiede zwischen den Listen.
- Versuche nun, die Funktion
reverse(liste)zu implementieren. Denk dabei an deine Antworten von der letzten Aufgabe. Schreibe die Funktion in das folgende Code-Fenster und teste sie mit verschiedenen Beispielen.
def reverse(liste):
# Dein Code hier
...
print(reverse([1, 2, 3, 4, 5]))
print(reverse([4711]))
print(reverse(['a', 'b', 'c']))
print(reverse([True, False, False]))

