Fachkonzept
Der Prozess der rekursiven Problemlösung, den du in den letzten Zwei Kapiteln vertieft hast, lässt sich oft in zwei Phasen unterteilen:
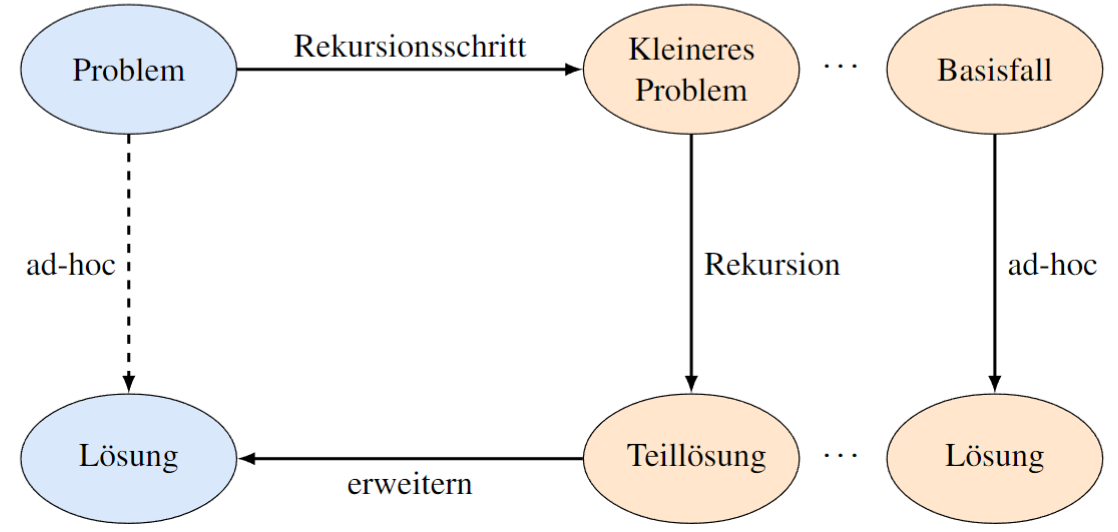
Rekursiver Abstieg
Das ist die Phase, in der wir uns dem Basisfall nähern. Bei jedem rekursiven Schritt wird das Problem kleiner gemacht. Beim Dateisuchbeispiel ist das das wiederholte "Betreten" eines Unterordners und das Fokussieren der Suche auf diesen kleineren Bereich. Die Problemlösung "steigt" sozusagen in die Tiefe der Ordnerstruktur hinab.
Bei anderen Problemen wie dem Berechnen der Fakultät oder das Aufsummieren aller Elemente einer Liste wird die Zahl immer kleiner, oder die Liste immer kürzer.
Rekursiver Aufstieg
Das ist die Phase, nachdem der Basisfall erreicht wurde. Die Information oder das Ergebnis des Basisfalls (z.B. "Datei (nicht) gefunden an Pfad X" oder "Summe aller Elemente einer leeren Liste ist gleich 0") wird zurückgegeben. Bei komplexeren rekursiven Problemen werden die Ergebnisse der kleineren Problem-Instanzen dann verwendet, um das Ergebnis für die nächstgrößere Instanz zu berechnen. Die Ergebnisse "steigen" sozusagen aus der Tiefe wieder auf. Wenn die Datei gefunden wurde, wird diese Information "nach oben" durch die Ordnerhierarchie gemeldet. Jenachdem kann dann weitergesucht werden oder die Suche beendet werden, falls die Datei gefunden wurde.
Bei der Fakultätsfunktion multiplizieren wir das Ergebnis des rekursiven Aufrufs mit der Zahl selbst, um auf die Fakultät der ursprünglichen Zahl zu kommen. Beim Aufsummieren der Elemente einer Liste addieren wir das erste Element der Liste mit dem Ergebnis des rekursiven Aufrufs, um auf die Summe aller Elemente der ursprünglichen Liste zu kommen.
Die "Magie der Rekursion"
Das Schema aus dem letzten Kapitel kann uns beim Programmieren rekursiver Funktionen helfen. Wenn wir eine rekursive Funktion schreiben, können wir gedanklich annehmen, dass unsere Funktion das um eins kleinere Problem "wie durch Zauberhand" bereits lösen kann. Deshalb nennen wir das auch die Magie der Rekursion. Dann überlegen wir uns, was wir mit dem Ergebnis des kleineren Problems noch machen müssen, um auf das Endergebnis zu kommen.
Für das Dateisuchbeispiel: Um herauszufinden, ob die Datei in einem aktuellen Ordner (oder dessen Unterordnern) ist, prüfen wir erst die Dateien direkt im aktuellen Ordner. Finden wir sie nicht, und es gibt Unterordner, sagen wir uns für jeden Unterordner: "Ich vertraue darauf, dass meine Suchmethode schon weiß, wie sie diese Datei in diesem Unterordner findet und mir das Ergebnis liefert."
Genauso können wir auch bei allen anderen Problemen vorgehen, die wir bereits gelöst haben. Wenn wir wie im vorherigen Kapitel eine Liste umkehren wollen, gehen wir davon aus, dass wir die um eins kürzere Liste bereits umkehren können und müssen uns dann nur noch überlegen, dass wir das übrige Element dann "nur noch" hinten an die Liste anhängen müssen.
Zusammengefasst müssen uns also beim rekursiven Lösen von Problemen die folgenden Schritte überlegen:
- Wie reduziere ich das Problem?
- Was mache ich mit dem Ergebnis des kleineren Problems unter der Annahme, dass die Funktion das kleinere Problem bereits lösen kann?
- Was ist die kleinste Instanz des Problems bzw. was ist der Basisfall (oder die Basisfälle)?
- Was ist die Lösung des Basisfalls?
Um die zweite Überlegung zu treffen, hilft es oft, sich zu überlegen, was die Lösung des ursprünglichen Problems ist - sofern das möglich ist.