Eine Verhaltensbeschreibung

Das Verhalten eines Algorithmus präzise beschreiben

Was leistet der Wechselwegnahme-Algorithmus?

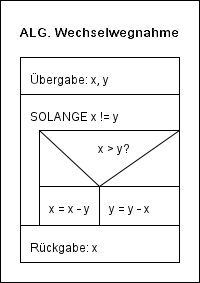
Betrachten wir zunächst einige Beispiele. Wenn für x die Zahl 15 und für y die Zahl 7 übergegeben werden, dann wird nach Ausführung der Anweisungen die Zahl 1 (für x) und die Zahl 1 (für y) erzeugt. Wir kürzen dies wie folgt ab:

vorher:  x = 15; y = 8
nachher: x = 1;  y = 1

Mit vorher bzw. nachher soll hier der Zustand nach der Übergabe bzw. vor der Rückgabe benannt werden.

Für das Verhalten des Algorithmus bei den Übergaben 10 und 21 erhält man:

vorher:  x = 20; y = 21
nachher: x = 1;  y = 1

Entsprechend ergibt sich für die Übergaben 3 und 20 das folgende Verhalten:

vorher:  x = 7;  y = 20
nachher: x = 1;  y = 1

Folgende Vermutung ist daher naheliegend:

vorher:  x = a;  y = b; a, b sind beliebige natürliche Zahlen
nachher: x = 1;  y = 1

Aber stimmt diese Vermutung auch? Weitere Beispiele zeigen, dass das nicht der Fall ist:

vorher:  x = 8;  y = 8
nachher: x = 8;  y = 8

Wenn die beiden eingegebenen Zahlen gleich sind, dann wird die Anweisung innerhalb der SOLANGE-Schleife nicht durchgeführt und die übergegebenen Zahlen bleiben unverändert.

Man könnte jetzt vermuten, dass immer dann Einsen erzeugt werden, wenn die übergegebenen Zahlen ungleich sind. Aber auch das stimmt nicht:

vorher:  x = 24; y = 15
nachher: x = 3;  y = 3

Die Sache ist also nicht ganz so leicht, wie es auf den ersten Blick erscheint. Weitere Beispiele lassen vermuten, dass der Algorithmus den größten gemeinsamen Teiler der beiden übergebenen Zahlen berechnet:

vorher:  x = a;  y = b; a, b sind beliebige natürliche Zahlen
nachher: x = y = ggT(a, b)

Auch diese Verhaltensbeschreibung ist noch nicht ganz korrekt. Wenn z.B. a = 0 und b > 0 gilt, dann gerät der Algorithmus in eine Endlosschleife.

Wir berücksichtigen das, indem wir eine Zusatzbedingung an die übergebenen Werte formulieren.

vorher:  x = a;  y = b; a, b sind beliebige natürliche Zahlen ungleich 0
nachher: x = y = ggT(a, b)

Mit dieser Beschreibung haben wir jetzt tatsächlich das Verhalten des Algorithmus korrekt beschrieben. Das lässt sich auch formal beweisen (so wie im Abschnitt Korrektheit verifizieren). Auf diesen mathematischen Beweis verzichten wir hier allerdings.

Wir betrachten vielmehr die Art und Weise, wie man das Verhalten eines Algorithmus mit einer sogenannten Spezifikation präzise beschreiben kann. Die Spezifikation besteht dabei aus einer Vorbedingung, die den Ausgangszustand beschreibt, sowie einer Nachbedingung, die den Endzustand beschreibt.

Eine Spezifikation wird manchmal in die Darstellung des Algorithmus integriert. Oft lässt man die für das Verhalten nicht relevanten Übergabe- und Rückgabeanweisungen weg und ergänzt stattdessen die Vor- und Nachbedingung.