Exkurs - Grenzen der rekursiven Verarbeitung bei realen Systemen

Näherung von pi nach Leibniz

Der Gelehrte Gottfried Wilhelm Leibniz entwickelte im 17 Jahrhundert eine Möglichkeit, die Kreiszahl π durch eine Reihe anzunähern. Je mehr Glieder der Reihe du berechnest und addierst, desto genauer wird das Ergebnis (das du dann noch mit 4 multiplizieren musst).

Die Leibniz-Reihe wird wie folgt berechnet:

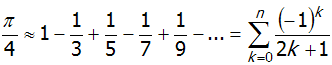
Der erste Summand ist also 1, dann folgt $-\frac{1}{3}$, dann $+\frac{1}{5}$, usw.

Die folgenden beiden Funktionen berechnen die Leibniz-Reihe bis zur angegebenen Grenze - einmal iterativ (also mit einer while-Wiederholung) und einmal rekursiv.

def Leibniz_iterativ(Grenze):
    """ Gibt eine Näherung für pi/4 zurück """
    ergebnis=0
    for k in range(0,Grenze+1):
        ergebnis = ergebnis + (-1)**k/(2*k+1)

    return ergebnis



def Leibniz_rekursiv(Grenze):
    if Grenze>0:
        ergebnis = (-1)**Grenze/(2*Grenze+1) + Leibniz_rekursiv(Grenze-1)
    else:
        ergebnis = (-1)**Grenze/(2*Grenze+1)

    return ergebnis

Aufgabe 1

Teste, ob die beiden Funktionen das gleiche Ergebnis liefern!

Ab wann stimmt der Wert für π mindestens bis zur zweiten Stelle? Schreibe ein Programm, das den Wert für diese Grenze automatisch ermittelt.

Aufgabe 2

Vielleicht hast du schon bemerkt, dass die rekursive Lösung ab einer bestimmten Grenze nicht mehr funktioniert:

Warum ist das so?

Warum begrenzt der Python-Interpreter die Rekursionstiefe?
Teste dafür den Aufruf der rekursiven Funktion einmal im Python-Tutor:

Du kannst auch einmal mit der Ausführung der iterativen Version im Python-Tutor vergleichen.