inf-schule | Fallstudie - Rekursive Verarbeitung von Listen » Anwendung

Anwendung - Verarbeitung geometrischer Objekte

Verwaltung und Verarbeitung geometrischer Objekte

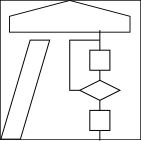
In den folgenden Aufgaben geht es um die Verwaltung und Verarbeitung geometrischer Objekte. Wir betrachten vereinfachend nur geometrische Objekte, die aus Streckenzügen mit Punkten mit ganzzahligen Koordinaten bestehen. Die folgende Abbildung (Logo des Fachbereichs Informatik der TU Kaiserslautern) ist aus solchen geometrischen Objekte aufgebaut.

Aufgabe 1

Geometrische Objekte können mit Hilfe von Listen dargestellt werden. Mache dir klar, wie dies im folgenden Quelltext zum oben gezeigten Logo gemacht ist.

stuetzelinks = [[0, 0],[20, 0],[50, 100],[30, 100],[0, 0]]
blockunten = [[90, 10],[110, 10],[110, 30],[90, 30],[90, 10]]
blockoben = [[90, 70],[110, 70],[110, 90],[90, 90],[90, 70]]
raute = [[80, 50],[100, 40],[120, 50],[100, 60],[80, 50]]
verbindung1 = [[100, 110], [100, 90]]
verbindung2 = [[100, 70], [100, 60]]
verbindung3 = [[100, 40], [100, 30]]
verbindung4 = [[100, 10], [100, 0]]
verbindung5 = [[80, 50], [70, 50], [70, 100], [100, 100]]
stuetzerechts = [verbindung1, blockoben, verbindung2, raute, \
                 verbindung5, verbindung3, blockunten, verbindung4]
dach = [[10, 110],[130, 110],[130, 125],[70, 140],[10, 125],[10, 110]]
tor = [stuetzelinks, stuetzerechts, dach]
rahmen = [[0, 0],[140, 0],[140, 140],[0, 140],[0, 0]]
logo = [tor, rahmen]

Welche Listenstruktur haben die einzelnen geometrischen Objekte? (stuetzelinks: Liste aus Listen, ...)

Aufgabe 2

Analysiere und teste die folgenden Funktionen. Beschreibe möglichst präzise, was sie leisten.

def istPunkt(L):
    if type(L) == list:
        if len(L) == 2:
            if (type(L[0]) == int) and (type(L[1]) == int):
                return True
            else:
                return False
        else:
            return False
    else:
        return False

def istStreckenzug(L):
    if type(L) == list:
        if len(L) == 0:
            return True
        else:
            if istPunkt(L[0]):
                return istStreckenzug(L[1:])
            else:
                return False
    else:
        return False

def istFigur(L):
    if type(L) == list:
        if len(L) == 0:
            return True
        else:
            if istStreckenzug(L[0]) or istFigur(L[0]):
                return istFigur(L[1:])
            else:
                return False
    else:
        return False

Aufgabe 3

Analysiere und teste auch die folgenden Prozeduren (zusammen mit den Programmteilen aus Aufgabe 1 und Aufgabe 2).

from turtle import *

def istPunkt(L):
    ...

def istStreckenzug(L):
    ...

def istFigur(L):
    ...

def zeichnePunktListe(punktListe):
    if punktListe != []:
        punkt = punktListe[0]
        t.goto(punkt)
        zeichnePunktListe(punktListe[1:])

def zeichneStreckenzug(streckenzug):
    if istStreckenzug(streckenzug):        
        if streckenzug != []:
            punkt = streckenzug[0]
            t.up()
            t.goto(punkt)
            t.down()
            zeichnePunktListe(streckenzug[1:])

def zeichneFigur(figur):
    if istFigur(figur):
        if figur != []:
            objekt = figur[0]
            if istStreckenzug(objekt):
                zeichneStreckenzug(objekt)
            else:
                zeichneFigur(objekt)
            zeichneFigur(figur[1:])

# Erzeugung eines Turtle-Objekts
t = Turtle()
# Initialisierung
t.left(90)
# Test
...
logo = [tor, rahmen]
zeichneFigur(logo)

Aufgabe 4

Mit Hilfe einer folgenden Funktionen soll eine beliebige geometrische Figur um einen bestimmten Betrag in x-Richtung verschoben werden.

Analysiere die bereits gegebenen Funktionsdefinitionen. Ergänze die noch fehlende Funktionsdefinition und teste gründlich.

def xVerschiebenPunkt(punkt, x):
    if istPunkt(punkt):
        return [punkt[0]+x, punkt[1]]

def xVerschiebenStreckenzug(streckenzug, x):
    if istStreckenzug(streckenzug):
        if streckenzug == []:
            return []
        else:
            punkt = streckenzug[0]
            restStreckenzug = streckenzug[1:]
            return [xVerschiebenPunkt(punkt, x)] + xVerschiebenStreckenzug(restStreckenzug, x)

def xVerschiebenFigur(figur, x):
    ...

Definiere analog Funktionen zur Verschiebung in y-Richtung und Funktionen zur Verschiebung in beide Richtungen. Teste die Funktionen mit verschiedenen geometrischen Objekten.

Aufgabe 5

Mit Hilfe einer Funktion soll eine beliebige geometrische Figur an der x-Achse gespiegelt werden.

Einfache Variante: Alle Punkte werden gespiegelt.

Schwierige Variante: Alle Punkte werden gespiegelt. Die Reihenfolge der Punkte eines Streckenzugs werden umgekehrt. Auch bei Gruppierungen wird die Reihenfolge der Objekte umgekehrt.

Aufgabe 6

Mit Hilfe geeigneter Funktionen soll die maximale x- bzw. y-Koordinate eine Figur bestimmt werden.

Entwickle eine geeignete Funktionsdefinition.

Aufgabe 7

Mit Hilfe einer Funktion soll bestimmt werden, ob eine geometrische Figur links von einer anderen geometrischen Figur liegt.