Einstieg - Wege im Galton-Brett
Wege im Galtonbrett
Ein Galton-Brett besteht aus Stäben, die in Reihen untereinander versetzt angeordnet sind.
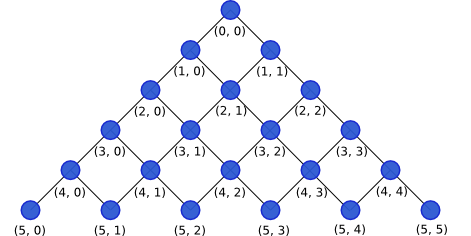
Wenn man eine Kugel ein solches Galton-Brett herunterrollen lässt, dann trifft es auf jeweils auf einen Stab und rollt dann entweder links oder rechts davon weiter herunter.
Die Stäbe in der Abbildung oben sind bereits mit Stab-Koordinaten versehen. Mit diesen Koordinaten könnte man einen möglichen Kugelweg so beschreiben: (0,0), (1, 0), (2, 1), (3, 1), (4, 1), (5, 2).
Aufgabe 1
Wie viele Wege gibt es im Galton-Brett bis zum Stab (m, n)? Bestimme für alle Stäbe erst einmal die jeweilige Anzahl. Zur Kontrolle: Bis zum Stab (5, 3) gibt es 10 Wege.
Aufgabe 2
Die Funktion galton(m, n) beschreibe die Anzahl der Wege im Galton-Brett bis zum
Stab (m, n). Begründe folgende Eigenschaften dieser Funktion:
- galton(n, 0) = 1
- galton(n, n) = 1
- galton(m, n) = galton(m-1, n-1) + galton(m-1, n), falls m > 0 und 0 < n < m gilt.
Aufgabe 3
Teste die folgenden Funktionsdefinitionen. Worin unterscheiden sie sich? Welche ist korrekt?
Version 1:
def galton(m, n):
if m < n:
return None
else:
if (n == 0) or (n == m):
return 1
else:
return (galton(m-1, n-1) + galton(m-1, n))
Version 2:
def galton(m, n):
if m < n:
return 0
else:
if n == 0:
return 1
else:
return (galton(m-1, n-1) + galton(m-1, n))
Version 3:
def galton(m, n):
if m == 0:
if n == 0:
return 1
else:
return 0
else:
if n == 0:
return 1
else:
return (galton(m-1, n-1) + galton(m-1, n))

