Übungen

Aufgabe 1

Ein Kapital von 1000 Euro wird jährlich mit 5% verzinst. Die Funktion kapital(n) beschreibe den Kapitalwert nach n Jahren.

Die folgenden Problemreduktionsschritte sollen dem Algorithmus / Programm zu Grunde liegen.

kapital(0) -> 
    1000

kapital(5) ->
    kapital(4) + 0.05 * kapital(4)

Verallgemeinere diese Reduktionsschritte zu einem Programm und teste es mit mehreren Funktionsaufrufen.

Aufgabe 2

Ein Patient nimmt jeden Morgen 5 mg eines Medikaments ein. Im Laufe des Tages werden von dem gesamten, im Körper befindlichen Medikament 40% abgebaut. Die Funktion medikamentenmenge(n) beschreibe die Menge des Medikaments (in mg), die sich am n-ten Tag morgens nach Einnahme des Medikaments im Körper befindet. Dabei soll die erste Einnahme am 0. Tag erfolgen.

Ergänze die folgenden Problemreduktionsschritte und verallgemeinere sie zu einem rekursiven Algorithmus / Programm.

medikamentenmenge(0) -> 
    ...

medikamentenmenge(5) ->
    ...

Aufgabe 3

Betrachte die in der Abbildung gezeigte Quadratpflanze.

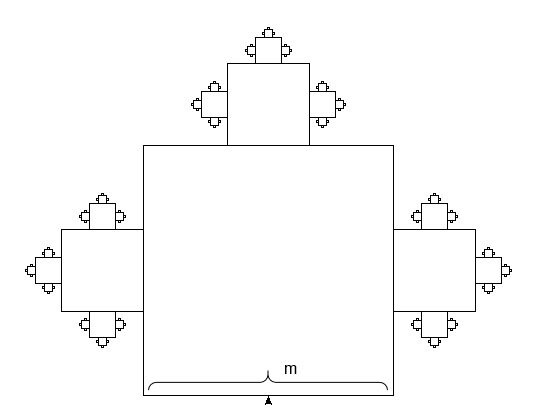
Im Jahr 0 besteht die Quadratpflanze nur aus dem großen Basisquadrat. Jedes Jahr wachsen dann neue kleinere Quadrate an drei Quadratseiten. Die Grundseite des Basisquadrates sei m Einheiten (z. B. cm) lang. Die Funktion umfang(n, m) beschreibe den Umfang der gesamten Quadratpflanze nach n Jahren bei einer Seitenlänge m. Die Funktion flaecheninhalt(n, m) beschreibe den Flächeninhalt der gesamten Quadratpflanze nach n Jahren bei einer Seitenlänge m. Entwickle rekursive Algorithmen zur Berechnung der beiden Funktionen. Welche Beobachtung kann man für die Entwicklung des Umfangs und der Fläche für große n machen?