Registermaschine als Berechnungsmodell
Rechnerarchitektur als Ausgangspunkt
Was liegt näher, als reale Rechner als Ausgangspunkt zu wählen, um die Idee "Computer" zu erfassen? Wir werden daher hier ein sehr einfaches, an der Architektur realer Rechner orientiertes Berechnungsmodell betrachten.
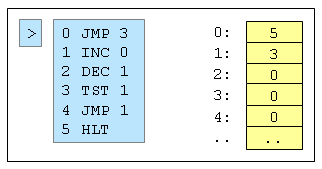
Eine Registermaschine ist eine Verarbeitungseinheit, die beliebig viele Register zur Speicherung von Daten hat und durch maschinennahe Programme gesteuert wird.
Die Register können natürliche Zahlen als Daten aufnehmen. Jedes Register hat eine Adresse - das ist eine natürliche Zahl, mit der man das Register eindeutig beschreiben kann.
Die Befehle der maschinennahen Programmiersprache sind in der folgenden Tabelle aufgelistet.
| Befehl | Bedeutung |
|---|---|
| i INC n | erhöhe Register n um 1; gehe zur Programmzeile i+1 |
| i DEC n | erniedrige (wenn möglich) Register n um 1; gehe zur Programmzeile i+1 |
| i JMP j | gehe zur Programmzeile j |
| i TST n | wenn Register n ungleich 0 ist, dann gehe zur Programmzeile i+1, sonst zur Programmzeile i+2 |
| i HLT | beende die Bearbeitung |
Ein Registermaschinenprogramm besteht aus einer endlichen Folge von Befehlen. Beachte, dass die Befehle von 0 an durchnummeriert werden.
Zur Abarbeitung von Registermaschinenprogrammen hat die Registermaschine einen Befehlszähler (in der Abbildung oben durch eine Markierung angedeutet), mit dem sie den aktuell zu bearbeitenden Befehl verwaltet.
Aufgabe 1
Was leistet das Registermaschinenprogramm in der Abbildung?
Aufgabe 2
Ändere das Registermaschinenprogramm in Aufgabe 1 so ab, dass folgende Addition ausgeführt wird: Vor der Ausführung befinden sich die zu addierenden natürlichen Zahlen in den Register R1 und R2. Nach der Ausführung befindet sich die Summe im Register R0.
Fachkonzept - Registermaschinen-Berechenbarkeit
Wir präzisieren den Begriff der Registermaschinen-Berechenbarkeit nur für Funktionen von N nach N.
Eine (k-stellige) Funktion f: N, ..., N -> N heißt Registermaschinen-berechenbar genau dann, wenn gilt: Es gibt eine Registermaschine mit der folgenden Eigenschaft:
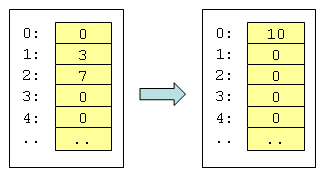
Ausgangszustand: In den Registern R1, ..., Rk befinden sich die zu verarbeitenden natürlichen Zahlen.
Fall 1: f(n1, ..., nk) ist definiert.
Zielzustand: Die Registermaschine hält und in R0 befindet sich der Funktionswert f(n1, ..., nk).
Fall 2: f(n1, ..., nk) ist nicht definiert.
Zielzustand: Die Registermaschine hält nicht.
In Aufgabe 2 hast du gezeigt, dass die Additionsfunktion auf natürlichen Zahlen Registermaschinen-berechenbar ist.
Aufgabe 3
Zeige, dass die folgenden Funktionen Registermaschinen-berechenbar sind. Suche dir ein Berechnungsproblem aus und entwickle ein geeignetes Registermaschinenprogramm.
(a) Subtraktionsproblem: Berechnet werden soll die Subtraktionsfunktion f: N, N -> N mit f(n1, n2) = n1 - n2, sofern n1 größer oder gleich n2 ist, bzw. f(n1, n2) ist nicht definiert, sofern n1 kleiner als n2 ist.
(b) Verdopplungsproblem: Berechnet werden soll die Verdopplungsfunktion f: N -> N mit f(n) = 2*n.
(c) Multiplikationsproblem: Berechnet werden soll die Multiplikationsfunktion f: N, N -> N mit f(n1, n2) = n1 * n2.
(d) Divisionsproblem: Berechnet werden soll die Divisionsfunktion f: N, N -> N mit f(n1, n2) = n1 // n2, sofern n2 ungleich 0 ist, bzw. f(n1, n2) ist nicht definiert, sofern n2 gleich 0 ist.
Aufgabe 4
Gibt es Funktionen, die Turingmaschinen-berechenbar sind und nicht Registermaschinen-berechenbar, oder umgekehrt? Was vermutest du?

