Automatisierte Programmanalyse
Ein Analyseprogramm für Ungeduldige
Zur Lösung des Halteproblems soll eine Python-Funktion istHaltend entwickelt werden,
mit deren Hilfe man Endlosschleifen bei beliebigen Python-Programmen feststellen kann.
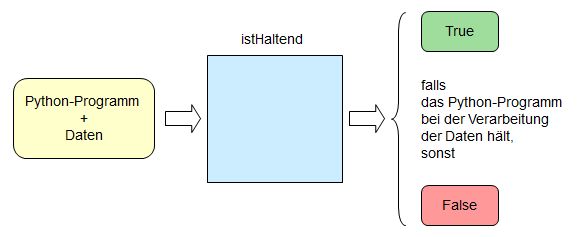
Wenn eine geeignete Funktionsdefinition für die Funktion istHaltend entwickelt ist,
dann kann man mit dieser Funktion künftig Endlosschleifen verhindern.
While-Analyse
Wann treten Endlosschleifen auf? Sicher nicht, wenn das Programm keine Wiederholungsanweisungen und keine Rekursion enthält. Kritisch kann es demnach nur werden, wenn bestimmte Programmkonstrukte im Programm vorkommen.
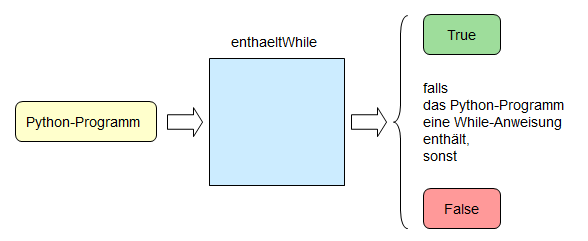
Wir untersuchen im Folgenden, ob ein Python-Programm eine while-Anweisung enthält.
Python-Programme sollen dabei immer in Form von Funktionsdefinitionen gegeben sein.
Beispiel:
Ein erstes Analyseprogramm
Hier ein erster Versuch zur Realisierung der Funktion enthaeltWhile.
Aufgabe 1
(a) Teste die Funktion enthaeltWhile mit verschiedenen Python-Quelltexten
und kontrolliere die Ergebnisse.
(b) Welches Problem ergibt sich hier? Wie könnte man das Problem lösen?
Ein verbessertes Analyseprogramm
Hier ein Vorschlag für ein verbessertes Analyseprogramm:
Aufgabe 2
(a) Welche Logik nutzt diese Funktionsdefinition? Teste die Funktion mit verschiedenen Beispielquelltexten.
(b) Teste auch den Fall, dass die Funktion enthaeltWhile den eigenen Quelltext analysiert.
Aufgabe 3
Beurteile den eingeschlagenen Weg, die Existenz von Endlosschleifen über Eigenschaften des Quelltextes herauszufinden. Wie vielversprechend ist dieser Weg?
Für deine Argumentation kannst du die folgenden Beispielprogramme verwenden: Programm 1 hält bei jeder Eingabe, bei Programm 2 weiß man nicht, ob es für jede Eingabe hält und Programm 3 hält nicht, wenn die Eingabe n größer als 3 ist.
Die Programme (in Form von Funktionsdefinitionen) benutzen alle die Hilfsfunktion primzahl.
def primzahl(n):
if n == 1:
prim = False
else:
prim = True
i = 2
while i <= n-1:
if n % i == 0:
prim = False
i = i+1
return prim
Programm 1: nächste Primzahl
def naechstePrimzahl(n):
gefunden = False
while not gefunden:
if primzahl(n):
gefunden = True
else:
n = n+1
return n
Programm 2: nächstes Primzahlzwillingspaar
def naechstesPrimzahlzwillingspaar(n):
gefunden = False
while not gefunden:
if primzahl(n) and primzahl(n+2):
gefunden = True
else:
n = n+1
return (n, n+2)
Programm 3: nächste nicht zu einer 6er Zahl benachbarte Primzahl
def naechsteNichtZu6erZahlBenachbartePrimzahl(n):
gefunden = False
while not gefunden:
if primzahl(n) and ((n+1)%6 > 0) and ((n-1)%6 > 0):
gefunden = True
else:
n = n+1
return n

