Turingmaschinen-Berechenbarkeit
Fachkonzept - Turingmaschinen-berechenbar
Nachdem im letzten Abschnitt das Verarbeitungsmodell "Turingmaschine" präzisiert wurde, soll jetzt geklärt werden, was man unter "Lösbarkeit mit einer Turingmaschine" versteht.
Zur Verdeutlichung betrachten wir das folgende Invertierproblem:


Auf dem Band befindet sich zunächst das zu verarbeitende Wort (Symbolfolge) - hier das Wort "101011#". Die Symbole des Wortes sind in aufeinander folgenden Feldern des Bandes abgelegt. Der Lese-Schreib-Kopf befindet sich auf dem ersten Symbol des Wortes.
Die beabsichtigte Verarbeitung von Symbolfolgen kann mit einer Funktion f beschrieben werden, die bestimmten Symbolfolgen (bestehend aus Symbolen einer vorgegebenen Symbolmenge) neue Symbolfolgen zuordnet, für bestimmte Symbolfolgen aber auch nicht definiert sein kann. Solche Funktionen werden auch partiell definierte Funktionen genannt.
Beim vorliegenden Invertierproblem ordnet die Funktion f der Symbolfolge "101011#" die neue Symbolfolge "010100#" zu. Wenn die zu verarbeitende Symbolfolge keine 0-1-Folge mit abschließendem #-Symbol darstellt, dann soll die Funktion für diese Symbolfolge nicht definiert sein.
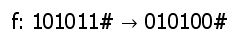
Die Lösbarkeit eines Problems mit einer Turingmaschine kann jetzt über die Berechenbarkeit der Funktion, die das Problem beschreibt, präzisiert werden.
Eine partiell definierte Funktion f, die (bestimmten) Symbolfolgen über einer vorgegebenen Symbolmenge neue Symbolfolgen zuordnet, heißt Turingmaschinen-berechenbar genau dann, wenn gilt: Es gibt eine Turingmaschine T mit der folgenden Eigenschaft:
Ausgangszustand: Auf dem Band befindet sich eine Symbolfolge w. Die Turingmaschine befindet sich im Anfangszustand, der Lese-/Schreibkopf am Anfang der Symbolfolge.
Fall 1: f(w) ist definiert.

Zielzustand: Die Turingmaschine T hält und hat f(w) auf dem Band erzeugt.

Fall 2: f(w) ist nicht definiert.

Zielzustand: Die Turingmaschine T hält nicht.
Im Folgenden soll der Berechenbarkeitsbegriff für Berechnungsprobleme mit natürlichen Zahlen spezialisiert werden.
Berechnungen mit natürlichen Zahlen
Zuerst betrachten wir die Addition von natürlichen Zahlen. Die beiden folgenden Abbildungen zeigen die Ausgangssituation mit zwei zu addierenden Zahlen (hier: 4+2) und die zu erreichende Zielsituation mit dem Rechenergebnis (hier: 6).


Beachte, dass die natürlichen Zahlen als Strichzahlen dargestellt werden. Man nennt eine solche Darstellung auch unäre Darstellung. Wir benutzen das Symbol "#" zur Darstellung des Rechenzeichens (hier interpretiert als "+").
Wie kann eine Turingmaschine dieses Rechenproblem lösen?
Eine sehr einfache Möglichkeit besteht darin, nach rechts zu laufen, bis das Rechenzeichen "#" gefunden wird. Dieses Rechenzeichen wird dann durch einen Strich (in der Abbildung mit dem Symbol "1" dargestellt) ersetzt. Anschließend läuft man nach links bis zum Anfang der Strichreihe und entfernt den ersten Strich.
Aufgabe 1
Entwickle ein geeignetes Steuerprogramm für das Additionsproblem.
Aufgabe 2
Entwickle ein geeignetes Steuerprogramm für eines der folgenden Rechenprobleme:
(a) Subtraktionsproblem: Das Symbol "#" wird als "minus" gedeutet. Das Rechenergebnis soll die Differenz der beiden vorgegebenen Strichzahlen darstellen. Wenn die erste Strichzahl kleiner als die zweite Strichzahl ist, dann soll die Turingmaschine nicht mehr klarkommen und in einer Endlosschleife irgendetwas machen.
(b) Verdopplungsproblem: Hier wird das Symbol "#" nicht benötigt. Das Rechenergebnis soll das Doppelte einer vorgegebenen Strichzahl darstellen.
(c) Multiplikationsproblem: Das Symbol "#" wird als "mal" gedeutet. Das Rechenergebnis soll das Produkt der beiden vorgegebenen Strichzahlen darstellen.
(d) Divisionsproblem: Das Symbol "#" wird als "durch" gedeutet. Das Rechenergebnis soll den ganzzahligen Quotienten (ohne Rest) der beiden vorgegebenen Strichzahlen darstellen. Wenn die zweite Strichzahl eine Null ist, dann soll die Turingmaschine nicht mehr klarkommen und in einer Endlosschleife irgendetwas machen.
Beschreibung von Problemen mit Hilfe von Funktionen
Rechenprobleme lassen sich mit Hilfe von Funktionen beschreiben.
Als erstes Beispiel betrachten wir noch einmal die Addition natürlicher Zahlen.
Das Addierproblem besteht darin, aus zwei vorgegebenen natürlichen Zahlen n1, n2 die Summe dieser Zahlen n1 + n2 zu erzeugen.


Formal lässt sich die gewünschte Erzeugung durch die Addierfunktion f: N, N -> N mit f(n1, n2) = n1 + n2 erfassen. Diese Funktion beschreibt die Addition natürlicher Zahlen, z.B. durch f(4,2) = 6.
Als zweites Beispiel betrachten wir die Subtraktion natürlicher Zahlen. Die folgende Abbildung zeigt als möglichen Ausgangszustand die "Rechensituation 2-4".

Wenn man ausschließlich mit natürlichen Zahlen rechnet, dann ergibt sich hier die Schwierigkeit, dass kein Rechenergebnis für die vorgegebene Rechensituation existiert. Wir berücksichtigen dies, indem wir Funktionen betrachten, die nur teilweise (man sagt auch partiell) definiert sind.
Das Subtraktionsproblem lässt sich durch die folgende partiell definierte Subtraktionsfunktion f: N, N -> N beschreiben:
n1 - n2, falls n1 ≥ n2 f(n1, n2) = nicht definiert, falls n1 < n2
In den bisher betrachteten Beispielen wurden jeweils 2-stellige (partielle) Funktionen f: N, N -> N zur Problembeschreibung benutzt. Es gibt zahlreiche Probleme, deren Beschreibung zu einer 1-stelligen (partiellen) Funktion f: N -> N führen. Als Beispiel sei das Verdopplungsproblem genannt, das mit der Funktion f: N ->N mit f(n) = 2*n beschrieben wird. Des weiteren gibt es Probleme, die mit einer 3-stelligen (partiellen) Funktion f: N, N, N -> N oder einer 4-stelligen (partiellen) Funktion f: N, N, N, N -> N usw.. adäquat beschrieben werden. Wir betrachten daher im Folgenden beliebige k-stellige (partielle) Funktionen f: N, ..., N -> N.
Turingmaschinen-Berechenbarkeit für Funktionen über den natürlichen Zahlen
Wir konkretisieren den Begriff der Turing-Berechenbarkeit jetzt für k-stellige partiell definierte Funktionen f: N,...,N -> N.
Solche Funktionen ordnen jedem k-Tupel aus natürlichen Zahlen eine natürliche Zahl oder den Wert nicht definiert
zu.
Eine k-stellige Funktion f: N,...,N -> N heißt Turingmaschinen-berechenbar genau dann, wenn gilt: Es gibt eine Turingmaschine T mit der folgenden Eigenschaft:
Ausgangszustand: Auf dem Band befindet sich ein k-Tupel (n1, ..., nk) aus natürlichen Zahlen n1, ..., nk, die alle als Strichzahlen dargestellt sind und mit dem Symbol "#" verbunden sind. Die Turingmaschine befindet sich im Anfangszustand, der Lese-/Schreibkopf am Anfang der Strichzahl.

Fall 1: f(n1, ..., nk) ist definiert.
Zielzustand: Die Turingmaschine T hält und hat f(n1, ..., nk) als Strichzahl auf dem Band erzeugt.

Fall 2: f(n1, ..., nk) ist nicht definiert.
Zielzustand: Die Turingmaschine T hält nicht.
Beispiele
Die Addierfunktion f: N, N -> N mit f(n1, n2) = n1 + n2 ist Turingmaschinen-berechenbar.
Die Subtraktionsfunktion f: N, N -> N mit f(n1, n2) = n1 - n2 (sofern n1 größer oder gleich n2 ist) bzw. f(n1, n2) ist nicht definiert (andernfalls) ist Turingmaschinen-berechenbar.
Deutung von Problemen als Rechenprobleme
Rechenprobleme kann man allgemein so charakterisieren, dass aus bestimmten natürlichen Zahlen eine neue natürliche Zahl bestimmt wird. Auf den ersten Blick scheint es so, dass Rechenprobleme eher spezielle, in der Mathematik auftretende Probleme sind. Es zeigt sich aber, dass man sehr viele Probleme als Rechenprobleme deuten kann. Als Beispiel betrachten wir das folgende Entscheidungsproblem.
Gegeben ist eine Zeichenkette aus Großbuchstaben des Standardalphabets A, B, C, ..., Z, z.B. die Zeichenkette "TURING". Gegeben ist zusätzlich ein Buchstabe des Alphabets, z.B. der Buchstabe "E". Das Problem soll darin bestehen, zu überprüfen, ob der vorgegebene Buchstabe in der gegebenen Zeichenkette vorkommt. Im vorliegenden Beispiel erhält man als Ergebnis ein "nein".
Mit Hilfe von Codierungen lässt sich aus dem beschriebenen Problem ein Rechenproblem erzeugen. Die Buchstaben des Alphabets sollen dabei wie folgt codiert werden:
A -> 1, B -> 2, C -> 3, ..., Z -> 26
Zur Codierung von Zeichenketten werden Buchstabencodes wie folgt zu natürlichen Zahlen zusammengefügt:
T U R I N G <- TURING | | | | | | 20 21 18 09 14 07 -> 202118091407
Zudem sollen die zu erzeugenden Ergebnisse "ja" bzw "nein" mit den Zahlen 1 bzw. 0 codiert werden.
Das oben beschriebene Entscheidungsproblem kann jetzt als Rechenproblem aufgefasst werden. Aus den Zahlen (5, 202118091407) für "kommt der Buchstabe E in der Zeichenkette TURING vor" soll die Zahl 0 für "nein" berechnet werden.
Aufgabe 3
Wie könnte man das folgende Problem in ein Rechenproblem überführen?
Gegeben: Schwarz-Weiß-Bild im PBM-Format
Gesucht: invertiertes Bild

