Lösungen zum Neun-Punkte-Problem
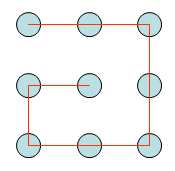
Eine Lösung mit 5 Strecken
Das schafft ja wohl jeder!
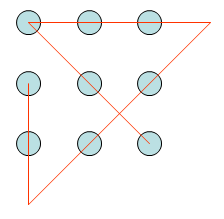
Eine Lösung mit 4 Strecken
Das ist eigentlich auch ganz einfach, oder?
Bist du (ohne Hilfen) auf die Lösung gekommen? Wenn nicht, woran hat das gelegen?
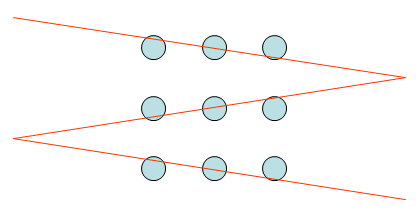
Eine Lösung mit 3 Strecken
Auch das geht - mit etwas Kreativität:
Zur Lösbarkeit des Neun-Punkte-Problems
Die oben gezeigten Lösungen des Neun-Punkte-Problems mit 4 bzw. 3 Strecken benutzen "Tricks": Der Streckenzug verlässt das vorgegebene Punktegitter und verläuft im Fall von 3 Strecken nicht genau durch die Punktmitten.
Es stellt sich hier sofort die Frage, ob das eigentlich erlaubt ist.
Das ist hier gar nicht so leicht zu beantworten. Bei der Formulierung des Problems wurde versäumt, die erlaubten Operationen zur Lösung des Problems zu präzisieren.
Nebenbei bemerkt: Natürlich liegt gerade darin der Reiz des Problems. Man kann kreativ Lösungsansätze entwickeln.
Aufgabe 1
Kannst man das Neun-Punkte-Problem mit vier Strecken auch dann noch lösen, wenn alle Eckpunkte des Streckenzugs zum vorgegebenen Punktegitter gehören und die Streckenzüge nur durch die Punktmitten verlaufen?

