Lösbarkeit des Halteproblems
Annahme: Das Halteproblem ist lösbar
Das Halteproblem besteht darin, eine Funktion (mit Funktionsdefinition) zu entwickeln, mit der man testen kann, ob eine übergebene Funktion bei der Verarbeitung übergebener Daten hält oder nicht.
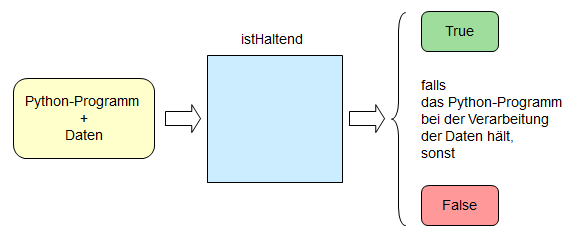
Wir zeigen jetzt, dass es keine Funktionsdefinition (in Python) für die Funktion istHaltend geben kann.
Hierzu nehmen wir an, dass es eine solche Funktiondefinition gibt:
def istHaltend(quelltext, daten):
...
return ...
Umkehrung des Halteverhaltens
Wenn es eine Funktionsdefinition (in Python) für die Funktion istHaltend gibt,
dann lässt sich die etwas seltsame Funktion umkehrHalteverhalten erstellen:
def umkehrHalteverhalten (quelltext):
def istHaltend(quelltext, daten):
...
return ...
if istHaltend(quelltext, quelltext) == True:
while True:
pass
else:
return False
Diese Funktion hat das folgende Verhalten:
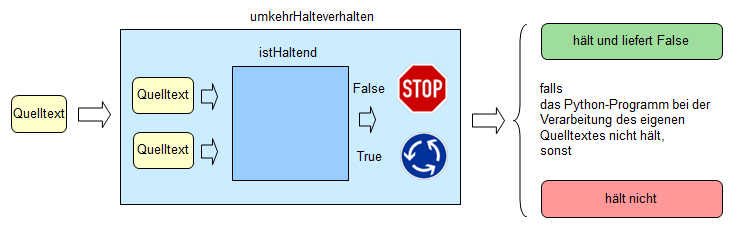
Verarbeitung des eigenen Quelltextes
Wir lassen jetzt die Funktion umkehrHalteverhalten ihren eigenen Quelltext verarbeiten.
# Funktionsdefinitionen
def umkehrHalteerhalten(quelltext):
def istHaltend(quelltext, daten):
...
return ...
if istHaltend(quelltext, quelltext) == True:
while True:
pass
else:
return False
# Funktionsaufruf
quelltextUmkehrHalteverhalten = """
def umkehrHalteverhalten(quelltext):
def istHaltend(quelltext, daten):
...
return ...
if istHaltend(quelltext, quelltext) == True:
while True:
pass
else:
return False
"""
print(umkehrHalteverhalten(quelltextUmkehrHalteverhalten))
Welches Ergebnis liefert die Funktion umkehrHalteverhalten in diesem speziellen Fall?
Die Antwort hierauf ist höchst seltsam.
Fall 1: Wir nehmen an, dass die Funktion umkehrHalteverhalten bei der Verarbeitung des eigenen Quelltextes hält.
Dann liefert istHaltend(quelltextUmkehrHalteverhalten, quelltextUmkehrHalteverhalten) den Wert True.
Die Funktion umkehrHalteverhalten gerät dann aber in eine Endlosschleife - und hält folglich nicht.
Fall 2: Wir nehmen an, dass die Funktion umkehrHalteverhalten bei der Verarbeitung des eigenen Quelltextes nicht hält.
Dann liefert istHaltend(quelltextUmkehrHalteverhalten, quelltextUmkehrHalteverhalten) den Wert False.
Die Funktion umkehrHalteverhalten liefert dann ebenfalls das Ergebnis False.
Das bedeutet aber, dass die Funktion hält - im Gegensatz zur gemachten Annahme.
In beiden Fällen verwickelt man sich in Widersprüche.
Auflösung des Widerspruchs
Wir sind von der Annahme ausgegangen, dass es eine Funktionsdefinition für die Funktion istHaltend gibt.
Aufbauend auf diese Annahme haben wir eine etwas merkwürdige Funktion umkehrHalteverhalten entwickelt. Bei der Analyse
des Verhaltens dieser merkwürdigen Funktion verwickelt man sich in Widersprüche.
Die Ursache der Widersprüche kann nur in der getroffen Annahme liegen. Die Annahme, dass es eine Funktionsdefinition
für die Funktion istHaltend gibt, muss daher falsch sein.

