Das Halteproblem

Halteproblem für Turingmaschinen

In Abschnitt Zusammenfassung - Lösbarkeit des Halteproblems haben wir die folgende Version des Halteproblems betrachtet:

Halteproblem für Python-Programme: Kann man ein Python-Programm entwickeln, mit dem man testen kann, ob ein übergebenes Python-Programm bei der Verarbeitung übergebener Daten hält oder nicht?

Wir sind eigentlich an der verallgemeinerten Version des Halteproblems interessiert:

Halteproblem für beliebige Algorithmen: Kann man einen Algorithmus entwickeln, mit dem man testen kann, ob ein (in geeigneter Weise codierter) übergebener Algorithmus bei der Verarbeitung übergebener Daten hält oder nicht?

Nach der Church-Turing-These können wir jeden Algorithmus durch eine geeignete Turingmaschine darstellen. Zu beachten ist dabei, dass die zu verarbeitenden Daten gegebenenfalls geeignet codiert werden müssen. Mit dieser Präzisierung des Algorithmusbegriffs können wir das Halteproblem jetzt so formulieren:

Halteproblem für Turingmaschinen: Kann man eine Turingmaschine entwickeln, mit der man testen kann, ob eine (in codierter Form) übergebene Turingmaschine bei der Verarbeitung übergebener Daten hält oder nicht?

Beschreibung mit einer Haltefunktion

Bisher haben wir (fast) ausschließlich Funktionen über den natürlichen Zahlen betrachtet. Wir bleiben bei diesen Funktionen und versuchen, das Halteproblem mit Hilfe natürlicher Zahlen zu codieren.

Aus Abschnitt Eine Aufzählung aller Turingmaschinen wissen wir bereits, dass alle Turingmaschinen über dem Eingabealphabet {I} und dem Bandalphabet {I, B} in der folgenden Weise aufgelistet werden können:

T0:   z0 B z0 B L; z0 I z0 B L;
T1:   z0 B z0 B L; z0 I z0 B R;
T2:   z0 B z0 B L; z0 I z0 I L;
T3:   z0 B z0 B L; z0 I z0 I R;
T4:   z0 B z0 B L; z0 I zS B L;
T5:   z0 B z0 B L; z0 I zS B R;
...

Im Folgenden wollen wir die Turingmschine T_i mit der zugehörigen Nummer i codieren.

Die zu verarbeiten Daten sind (evtl. auch leere) Folgen des Symbols "I". Diese Folgen können als Codierungen natürlicher Zahlen aufgefasst werden.

w0:   
w1:   I
w2:   II
w3:   III
w4:   IIII
w5:   IIIII
...

Mit der Funktion h soll jetzt das Halterverhalten von Turingmaschinen bei der Verarbeitung natürlicher Zahlen beschrieben werden.

Aufgabe 1

In der folgenden Wertetabelle sind bereits einige Funktionswerte von h eingetragen. Dabei werden die oben beschriebenen Codierungen zu Grunde gelegt.

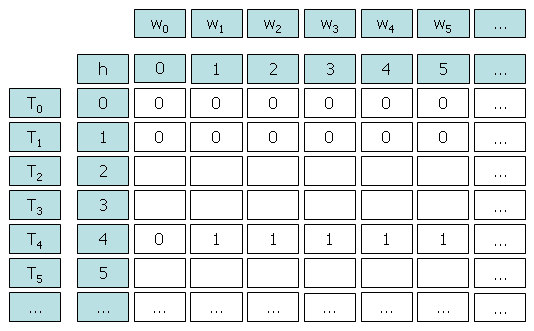
Ergänze die fehlenden Funktionswerte.

Argumentation mit einem Diagonalisierungsverfahren

Annahme: Es gibt eine Turingmaschine T_h, die die Funktion h berechnet.

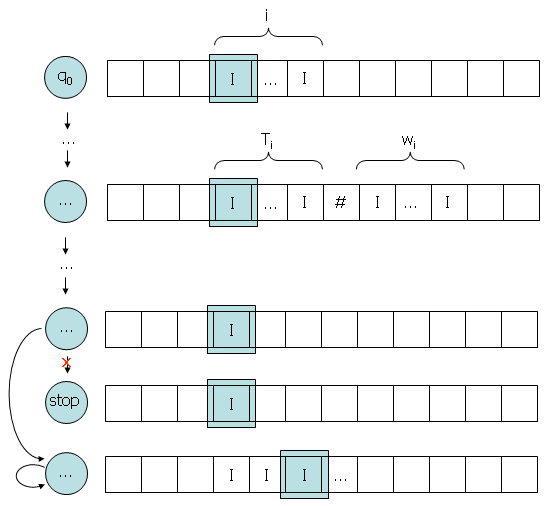
Die Abbildung verdeutlicht das Verhalten von T_h, wenn die übergebene Turingmschine bei dem übergebenen Wort hält.

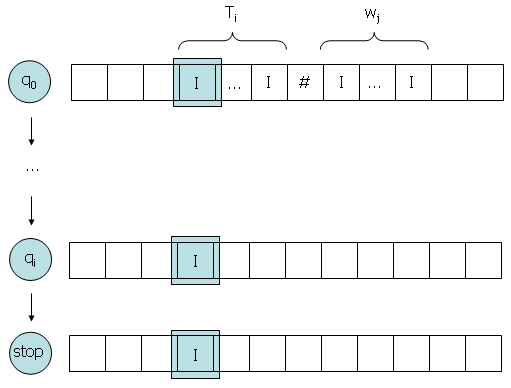
Wenn die übergebene Turingmschine bei dem übergebenen Wort nicht hält, dann erzeugt T_h ein leeres Band und geht in den Stop-Zustand über.

Wir benutzen jetzt ein Diagonalisierungsverfahren, um aus T_h eine neue Turingmaschine T zu konstruieren.

Die folgende Tabelle zeigt, wie das Halteverhalten aller möglichen Turingmaschinen bei bestimmten zu verarbeitenden Wörtern aussehen könnte.

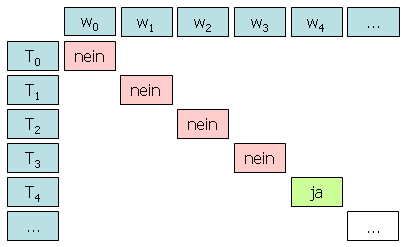
Wenn der Eintrag in der Tabelle zu einer bestimmten Turingmaschine und einem bestimmten Datum ein "ja" ist, dann soll die betreffende Turingmaschine bei der Verarbeitung des betreffenden Datums halten, bei "nein" entsprechend nicht.

Das Halteverhalten soll jetzt wie folgt umgekehrt werden.

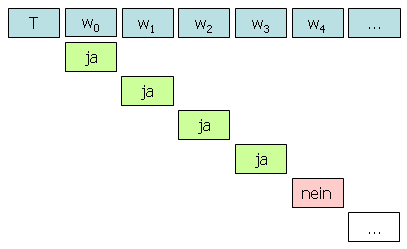
Ziel ist es, eine Turingmaschine T zu entwickeln, die dieses Halteverhalten zeigt. T soll also genau dann bei der Verarbeitung des Wortes w_i halten, wenn die Turingmaschine T_i bei der Verarbeitung des Wortes w_i nicht hält. T kehrt also das Halteverhalten der aufgelisteten Turingmaschinen in gewisser Weise um.

T gewinnen wir mit Hilfe von T_h, indem wir zunächst das zu verarbeitende Wort duplizieren, anschließend die dargestellte Zahl (i, i) von T_h verarbeiten lassen und abschließend den Übergang zum Stop-Zustand etwas abändern. Vorab wird geprüft, ob das gelesene Zeichen ein "I" ist. Wenn das der Fall ist, dann soll endlos ein "I" auf das Band geschrieben werden und eine Bewegung nach rechts erfolgen. Ist das gelesene Zeichen dagegen ein "B(lank)", dann soll ein Übergang in den Stop-Zustand erfolgen.

T entpuppt sich als höchst merkwürdige Turingmaschine: Einerseits muss T in der Auflistung aller Turingmaschinen vorkommen, also mit irgendeiner Turingmaschinen T_i der Auflistung übereinstimmen. Andererseits verhält sich T anders als jede der in der Auflistung vorkommenden Turingmaschinen. Es ergeben sich also zwei widersprüchliche Aussagen.

Die Annahme, dass es eine Turingmaschine T_h gibt, die die Funktion h berechnet, führt also zu einem Widerspruch. Die Annahme muss folglich falsch sein.