Ein zustandsbasiertes System zur Spracherkennung
Vereinfachte Gleitkommazahlen
Wir betrachten zunächst vereinfachte Gleitkommazahlen, die nach den folgenden Regeln gebildet werden.
kommazahl ::= intpart "." intpart intpart ::= digit+ digit ::= "0"|"1"|"2"
Solche Kommazahlen bestehen aus einer nichtleeren Folge von Ziffern gefolgt von einem Punkt und einer weiteren nichtleeren Folge von Ziffern. Hier einige Beispiele für solche Kommazahlen.
20.0 001.100 0.000
Zur Vereinfachung der Darstellung benutzen wir hier auch nur die Ziffern 0, 1 und 2.
Zustandsbasierte Spracherkennung
Die Spracherkennung bei den oben beschriebenen Kommazahlen lässt sich mit einem zustandsbasierten System durchführen, das sukzessive die einzelnen Zeichen der zu analysierenden Zeichenkette verarbeitet.
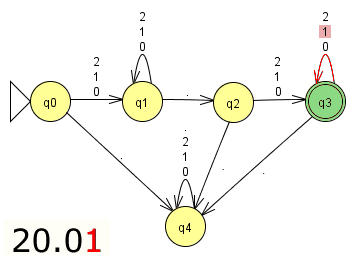
Zu Beginn befindet sich das System im Anfangszustand q0 (hier hervorgehoben durch das Dreieck).
Mit einer Ziffer gelangt man in den Zustand q1. In diesem Zustand bleibt man, wenn
weitere Ziffern folgen.
Mit einem Punkt geht es weiter in den Zustand q2.
Mit einer Ziffer gelangt man dann in den Zustand q3. In diesem Zustand bleibt man, wenn
weitere Ziffern folgen.
Der Zustand q3 ist als Endzustand markiert. Wenn die Verarbeitung einer Zeichenfolge in diesem
Zustand endet, dann liegt eine Kommazahl vor.
Keine Kommazahl liegt vor, wenn die Verarbeitung einer Zeichenfolge in einem Zustand endet, der kein Endzustand darstellt.
Klicke durch die Bildstrecke, um die Verarbeitung der Zahl 20.01 zu veranschaulichen!
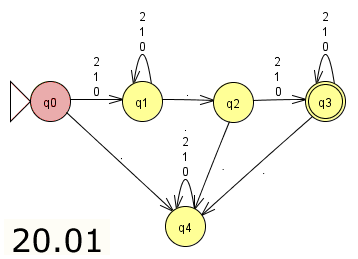
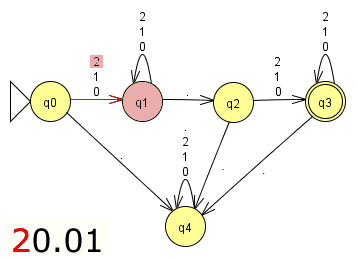
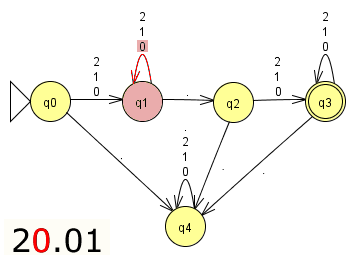
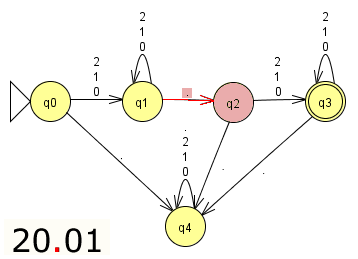

Aufgabe 1
Warum stellt eine Zeichenkette, die in den Zustand q4 führt, keine zu akzeptierende Kommazahl dar?
Experimente mit JFlap
Mit Hilfe des Software-Werkzeugs JFlap kann man die Worterkennung mit einem zustandsbasierten System experimentell testen.
Öffne zunächst mit [File][New][Finite Automaton] ein Eingabefenster für zustandsbasierte Systeme (endliche Automaten). In diesem Fenster kann man jetzt das zustandsbasierte System mit den vorgegebenen Button schrittweise aufbauen. Beachte, dass die Festlegung als Anfangs- oder Endzustand mit der rechten Maustaste erfolgt.
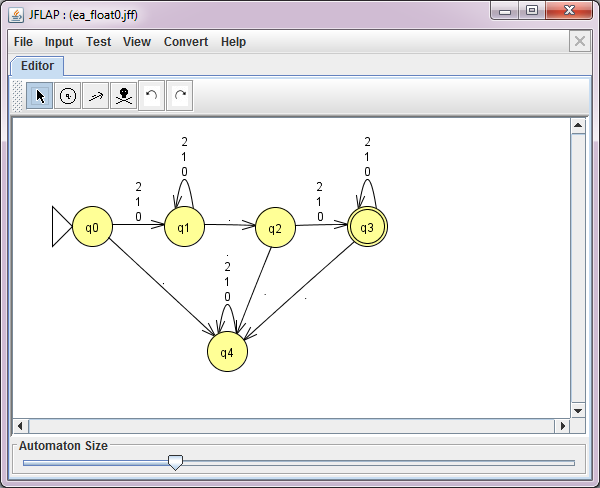
Zum Testen wählt man der Reihe nach die Menupunkte [Input][Step by State] oder [Input][Fast Run ...] aus.
In das [Input]-Feld gibt man die zu analysierende Zeichenfolge ein, z.B. 21.1.
Im "Step by State"-Fall kann man die Verarbeitung der eingegebenen Zeichfolge schrittweise durchspielen.
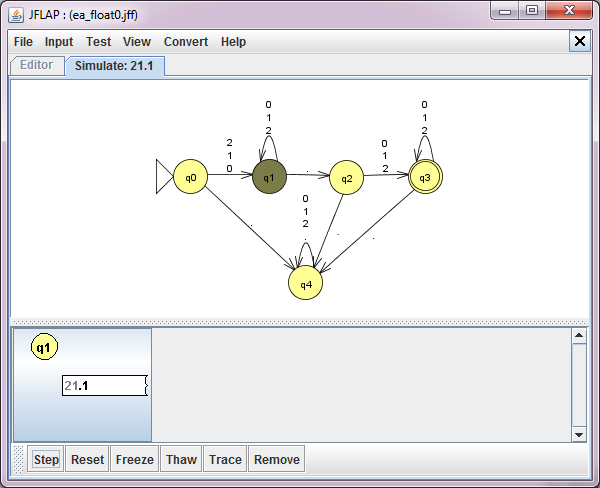
"Fast Runs" erhält man einen Überblick über die vollständige Verarbeitung der eingegebenen Zeichfolge.
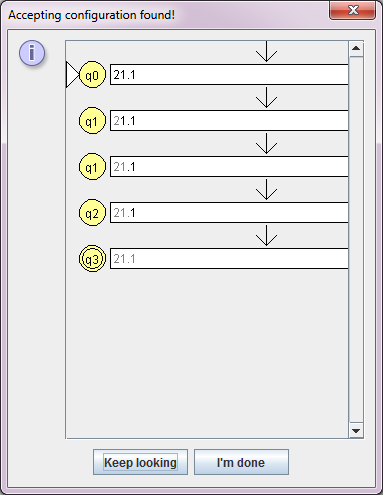
Aufgabe 2
Probiere das selbst mit verschiedenen Eingaben aus.
Beliebige Gleitkommazahlen
Wir betrachten zunächst Gleitkommazahlen ohne Exponenten. Die Grammatikregeln für diese Zahlen erhält man, indem man in den Grammatikregeln für Python-Gleitkommazahlen die Regeln für "exponentfloat" weglässt.
pointfloat ::= [intpart] fraction | intpart "." intpart ::= digit+ fraction ::= "." digit+ digit ::= "0"|"1"|"2"
Beispiele für "pointfloat"-Gleitkommazahlen:
20.0 001.100 0.000 .2 01.
Hier ein zustandsbasiertes System zur Erkennung von "pointfloat"-Gleitkommazahlen: ea_float1.jff.
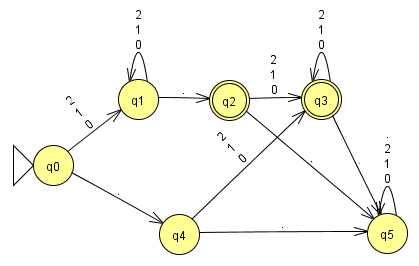
Beachte, dass ein solches System mehrere Endzustände haben kann.
Aufgabe 3
(a) Erkläre, warum das gezeigte zustandsbasierte System genau die "pointfloat"-Gleitkommazahlen erkennt.
(b) Vereinfache das zustandsbasierte System so, dass es mit nur einem Endzustand die "pointfloat"-Gleitkommazahlen erkennt.
Aufgabe 4
Betrachte jetzt beliebige Python-Gleitkommazahlen. Hier eine Grammatik (in EBNF) für diese Zahlen (mit eingeschränktem Ziffernbereich):
floatnumber ::= pointfloat | exponentfloat pointfloat ::= [intpart] fraction | intpart "." exponentfloat ::= (intpart | pointfloat) exponent intpart ::= digit+ fraction ::= "." digit+ exponent ::= "e" ["+" | "-"] digit+ digit ::= "0"|"1"|"2"
(a) Entwickle ein zustandsbasiertes System, das genau die beschriebenen Gleitkommazahlen erkennt.
(b) Teste das entwickelte System mit verschiedenen Eingaben. Teste insbesondere auch lange Eingaben. Warum kann das zustandsbasierte System auch lange Eingaben sehr schnell verarbeiten?

