Fachkonzept - Nichtdeterministischer Automat
Nichtdeterministische Automaten
Die Experimente mit JFlap zeigen, dass man aus einer regulären Grammatik G für eine Sprache L
einen endlichen Automaten AG automatisiert erzeugen kann, der diese Sprache akzeptiert.
Als Beispiel betrachten wir die Sprache LBin = {0, 1, 10, 11, 100, 101, 110, 111, 1000, ...}.
Diese Sprache lässt sich mit der regulärer Grammatik G beschreiben:
A -> 1B A -> 0C A -> 1C C -> λ B -> 0B B -> 1B B -> 0D B -> 1D D -> λ
Aus dieser Grammatik G kann folgender erkennender Automat AG erzeugt werden:
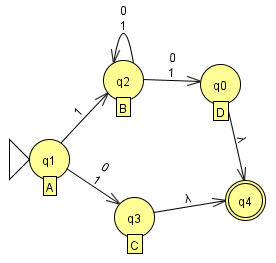
Der resultierende Automat ist kein endlicher Automat im bisherigen Sinne. Zwei Besonderheiten fallen direkt auf:
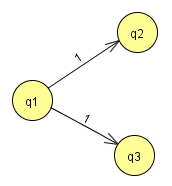
Der Automat ist nichtdeterministisch in dem Sinne, dass er zulässt, dass von einem Zustand aus bei derselben Eingabe Übergänge in unterschiedliche Folgezustände möglich sind.
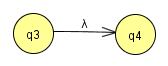
Zudem enthält der Automat Zustandsübergänge ohne Eingaben (sog. λ-Übergänge).
Einen endlichen Automaten, der nichtdeterministische Zustandsübergänge oder λ-Übergänge zulässt, nennt man nichtdeterministischen endlichen Automaten (kurz: NFA für nondeterministic finite automaton). Entsprechend nennt man einen endlichen Automaten, der keine nichtdeterministische Zustandsübergänge und keine λ-Übergänge enthält, einen deterministischen endlichen Automaten (kurz: DFA für deterministic finite automaton).
Spracherkennung mit nichtdeterministischen Automaten
Spracherkennung mit nichtdeterministischen Automaten funktioniert so ähnlich wie Spracherkennung mit deterministischen Automaten.
Man muss nur alle möglichen Zustandsübergänge für eine Eingabe durchspielen. Wenn nach der Verarbeitung des gesamten Eingabeworts ein Endzustand erreicht werden kann, dann gilt die Eingabe als akzeptiert, ansonsten als nicht akzeptiert.
Zusammenhang zwischen deterministischen und nichtdeterministischen Automaten
Nichtdeterministische Automaten sind allgemeiner konzipiert als deterministische Automaten.
Interessanterweise sind sie aber nicht mächtiger
.
Satz (über den Zusammenhang zwischen deterministischen und nichtdeterministischen Automaten):
Zu jedem nichtdeterministischen endlichen Automaten gibt es einen deterministischen
endlichen Automaten, der dieselbe Sprache erkennt. Man kann den deterministischen endlichen Automaten
automatisiert aus dem nichtdeterministischen endlichen Automaten erzeugen.
Bemerkung: Den Algorithmus zur Konstruktion des zu einem NFA äquivalenten DFA kann man sich von JFlap durchspielen lassen.

