Alternative Berechnungen
Ein alternatives Berechnungsverfahren entwickeln
Wir betrachten noch einmal das gitterförmige Wegenetz und die Funktion anzahlWege
zur Bestimmung der Anzahl der Wege vom Startpunt (0,0) zu einem Zielpunkt (n,k).
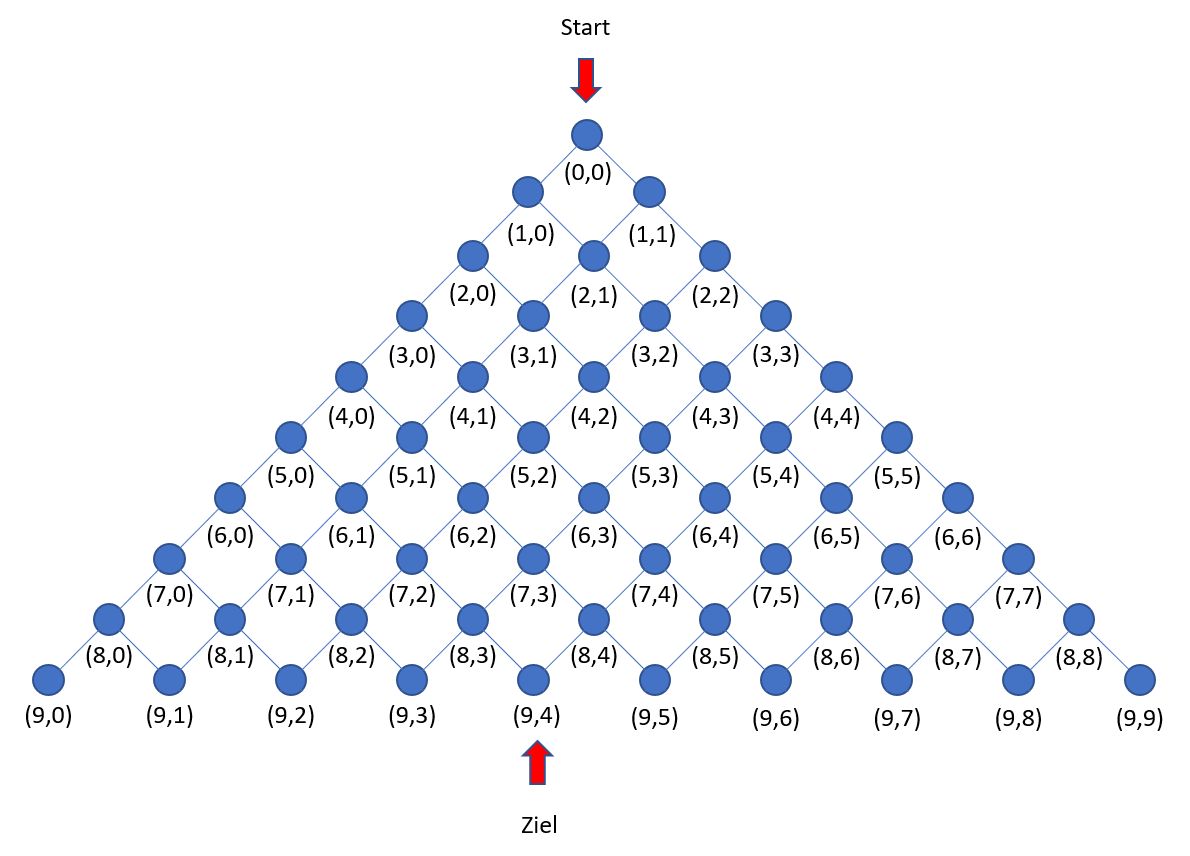
Ein interessante Beobachtung: Die Anzahl der Wege zu inneren Punkten kann man mit Quotienten aus geeignet gebildeten Produkten bestimmen.
anzahlWege 9 1 -> 9 = (9*8*7*6*5*4*3*2*1) // ((1) * (8*7*6*5*4*3*2*1)) anzahlWege 9 2 -> 36 = (9*8*7*6*5*4*3*2*1) // ((2*1) * (7*6*5*4*3*2*1)) anzahlWege 9 3 -> 84 = (9*8*7*6*5*4*3*2*1) // ((3*2*1) * (6*5*4*3*2*1)) anzahlWege 9 4 -> 126 = (9*8*7*6*5*4*3*2*1) // ((4*3*2*1) * (5*4*3*2*1)) anzahlWege 9 5 -> 126 = (9*8*7*6*5*4*3*2*1) // ((5*4*3*2*1) * (4*3*2*1)) anzahlWege 9 6 -> 84 = (9*8*7*6*5*4*3*2*1) // ((6*5*4*3*2*1) * (3*2*1)) anzahlWege 9 7 -> 36 = ... anzahlWege 9 8 -> 9 = ...
Aufgabe 1
- Kontrolliere die gezeigten Produktberechnungen.
- Ergänze analog die fehlenden Produktberechnungen.
- Kontrolliere mit weiteren Beispielen, ob man die Anzahl der Wege immer analog bestimmen kann.
Eine Produktfunktion
Zur Bestimmung der Anzahl der Wege benötigen wir eine Funktion,
die Produkte von Zahlen berechnet.
Solche Produkte sollen mit einer Funktion produkt bestimmt werden.
Signatur:
produkt: Int -> Int
Beispiele:
produkt 1 -> 1 = 1
produkt 2 -> 2 = 2*1
produkt 3 -> 6 = 3*2*1
produkt 4 -> 24 = 4*3*2*1
Aufgabe 2
-
Ergänze zunächst die folgende Reduktionsregel für konkrete Zahlenwerte.
Rekursionsschritt:
produkt 5 -> ... produkt 4
-
Ergänze die Reduktionsregeln für beliebige Zahlenwerte.
Rekursionsschritt:
Falls n > 1 ist: produkt n -> ...Rekursionsanfang:
Falls n == 1: produkt n -> ... -
Entwickle eine Funktionsdefinition für die Funktion
produktund teste sie in der REPL.produkt n = if n == 1 then ... else ...
Aufgabe 3
Mit Hilfe der Funktion produkt kann man die folgende Funktionsdefinition für die Funktion anzahlWege verwenden.
Vergleiche mit den Berechnungen ganz oben und teste diese Funktionsdefinition.
anzahlWege n k =
if k == 0 || k == n then
1
else
(produkt n) // ((produkt k) * (produkt (n - k)))
Ein weiteres Berechnungsverfahren
Die Anzahl der Wege zu inneren Punkten kann man auch so bestimmen.
anzahlWege 2 1 -> 2 = 2 // 1 anzahlWege 3 1 -> 3 = 3 // 1 anzahlWege 3 2 -> 3 = (3*2) // (2*1) anzahlWege 4 1 -> 4 = 4 // 1 anzahlWege 4 2 -> 6 = (4*3) // (2*1) anzahlWege 4 3 -> 4 = (4*3*2) // (3*2*1) anzahlWege 5 1 -> 5 = 5 // 1 anzahlWege 5 2 -> 10 = (5*4) // (2*1) anzahlWege 5 3 -> 10 = (5*4*3) // (3*2*1) anzahlWege 5 4 -> 5 = (5*4*3*2) // (4*3*2*1) anzahlWege 6 1 -> 6 = ... anzahlWege 6 2 -> 15 = ... anzahlWege 6 3 -> 20 = ... anzahlWege 6 4 -> 15 = ... anzahlWege 6 5 -> 6 = ... ... anzahlWege 9 4 -> 126 = ...
Im Nenner stehen in der Übersicht immer Produkte von Zahlen beginnend mit einer
Zahl n bis zur Zahl 1.
Solche Produkte können wir bereits mit der Funktion produkt bestimmen.
Im Zähler stehen in der Übersicht immer Produkte von Zahlen beginnend mit einer Zahl n bis hin zu einer Zahl m.
Solche Produkte sollen mit einer Funktion produktVonNbisM bestimmt werden.
Signatur:
produktVonNbisM: Int -> Int
Beispiele:
produktVonNbisM 5 5 -> 5
produktVonNbisM 5 4 -> 5*4
produktVonNbisM 5 3 -> 5*4*3
produktVonNbisM 5 2 -> 5*4*3*2
produktVonNbisM 5 1 -> 5*4*3*2*1
Aufgabe 4
-
Ergänze die Reduktionsregeln für die Funktion
produktVonNbisM.Rekursionsschritt:
Falls n > m ist: produktVonNbisM n m -> ... produktVonNbisM (n-1) mRekursionsanfang:
Falls n == m: produktVonNbisM n m -> ... -
Entwickle eine Funktionsdefinition für die Funktion
produktVonNbisMund teste sie in der REPL.produktVonNbisM n m = if n == m then ... else ... -
Nutze die Funktion
produktVonNbisMum eine Funktionsdefinition für die FunktionanzahlWegezu bestimmen.anzahlWege n k = if (k == 0) || (k == n) then 1 else ...

