Übungen - Verarbeitung von Zahlen
Aufgabe 1 (Summen von natürlichen Zahlen)
In dieser Aufgabe geht es um die Berechnung von Summen von natürlichen Zahlen.
0 0+1 0+1+2 0+1+2+3 0+1+2+3+4 ...
Hinweis: In ähnlicher Form hast du solche Summen bereits im Abschnitt zum Begrüßungsproblem betrachtet.
Ziel ist es, eine Funktion summe zu entwickeln, mit der man solche Summen bestimmen kann.
Signatur:
summe: Int -> Int
Beispiele:
summe 0 -> 0
summe 1 -> 1
summe 2 -> 3
summe 3 -> 6
...
(a) Im Rekursionsschritt reduziert man das Problem auf ein entsprechendes Problem in verkleinerter Form. Ergänze die Reduktionsregeln.
Rekursionsschritt (am Beispiel):
summe 5 -> ... (summe 4)
Rekursionsschritt (allgemein):
Falls n > 0 ist:
summe n -> ...
(b) Im Rekursionsanfang gibt man die Lösung des Problems für einen Startwert direkt an.
Rekursionsanfang:
Falls n == 0:
summe n -> ...
(c) Entwickle aus den Reduktionsregeln eine Funktionsdefinition für die Funktion summe und teste sie in der REPL.
Aufgabe 2 (lineares Wachstum)
Auf einem Konto befindet sich zu Beginn ein bestimmter Anfangsbetrag (z.B. 1000 €). Nach jedem Monat wird ein fester Betrag (z.B. 50 €) eingezahlt. Wie hoch ist der Kontostand nach einer vorgegebenen Anzahl von Monaten? Dieses Problem führt zu folgender Übergabe-Rückgabe-Situation:
Übergabe: - Anfangsbetrag: 1000 [€] - Einzahlungsbetrag: 50 [€] - Anzahl der Monate: 4 Rückgabe: - Kontostand nach Ablauf der Monate: 1200 [€]
(a) Mit der Funktion kontostand soll die Kapitalentwicklung auf dem Konto bestimmt werden.
Ergänze die bereits begonnene Modellierung der Funktion kontostand.
Signatur:
kontostand: ...
Beispiele:
kontostand 1000 50 4 -> 1200
kontostand ...
(b) Ergänze die Reduktionsregeln.
Rekursionsschritt (am Beispiel):
kontostand 1000 50 5 -> (kontostand 1000 50 4) ...
Rekursionsanfang:
kontostand 1000 50 0 -> ...
(c) Entwickle aus den Reduktionsregeln eine Funktionsdefinition für die Funktion kontostand und teste sie in der REPL.
Aufgabe 3 (exponentielles Wachstum)
Du hast 10.000 € angespart und legst das Geld in einem Aktion-Depot an, bei dem es jährlich 5% Rendite gibt. Gesucht ist die Entwicklung des Depotbestandes. Zur Klärung dieser Frage betrachten wir die folgende, etwas verallgemeinerte Übergabe-Rückgabe-Situation:
Übergabe: - Anfangsbetrag: 10000 [€] - Rendite in Prozent: 5 [%] - Anzahl der Jahre: 1 Rückgabe: - Depotstand nach Ablauf der Jahre: 10500 [€]
(a) Mit der Funktion depotstand soll die Depotentwicklung bestimmt werden.
Ergänze die bereits begonnene Modellierung der Funktion depotstand.
Signatur:
depotstand: ...
Beispiele:
depotstand 10000 5 1 -> 10500
depotstand ...
(b) Entwickle selbstständig geeignete Reduktionsregeln.
Rekursionsschritt (am Beispiel):
depotstand 10000 5 4 -> ...
Rekursionsanfang:
depotstand 10000 5 0 -> ...
(c) Entwickle aus den Reduktionsregeln eine Funktionsdefinition für die Funktion depotstand und teste sie in der REPL.
Aufgabe 4 (Fibonacci-Zahlen)
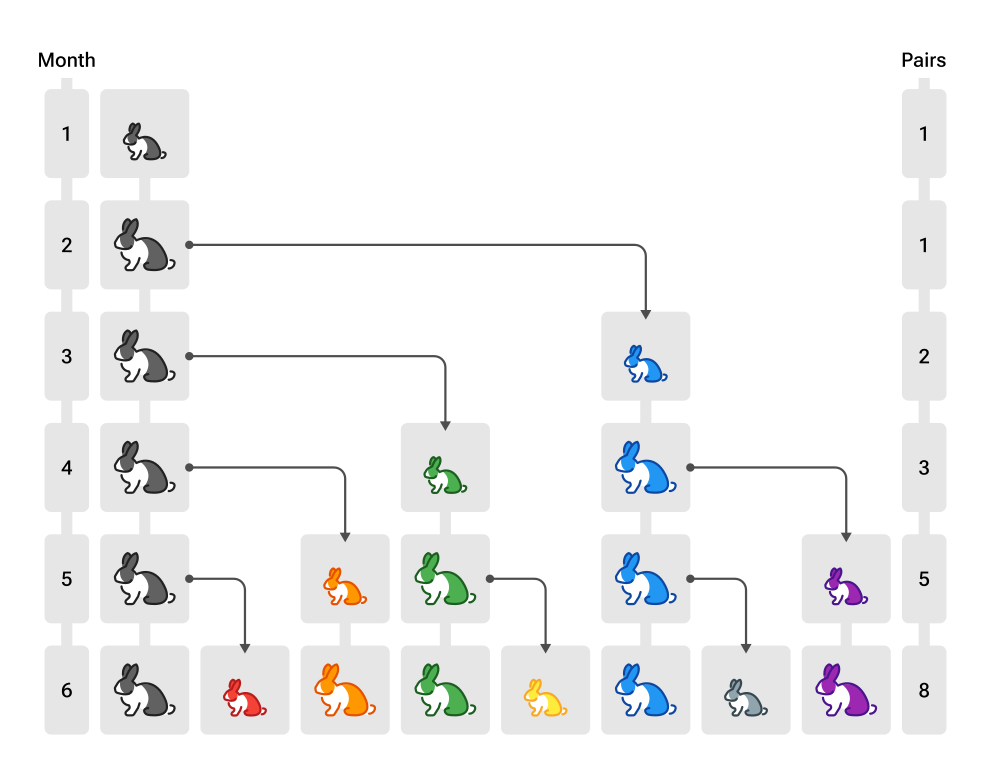
Der Rechenmeister Fibonacci - der um 1200 in Pisa lebte - hat sich mit einer Zahlenfolge beschäftigt, die man mit einer Kaninchenvermehrung verdeutlichen kann:
Die Kaninchenvermehrung erfolgt nach diesen Regeln:
- Zu Beginn gibt es $1$ Kaninchenpaar.
- Vom zweiten Lebensmonat an beginnt ein Kaninchenpaar sich fortzupflanzen.
- Jedes Kaninchenpaar erzeugt ein weiteres Paar pro Monat.
Zur Bestimmung der Anzahl der Kaninchenpaare betrachten wir diese Übergabe-Rückgabe-Situation:
Übergabe: - Monat: 6 Rückgabe: - Anzahl der Kaninchenpaare zu Beginn des Monats: 8
(a) Mit der Funktion fibonacci soll die Entwicklung der Kaninchenpopulation bestimmt werden.
Signatur:
fibonacci: Int -> Int
Beispiele:
fibonacci 1 -> 1
fibonacci 2 -> 1
...
fibonacci 6 -> 8
...
(b) Erkläre die Reduktionsregeln. Erkläre dabei auch, warum man 2 Regeln für den Rekursionsanfang benötigt.
Rekursionsschritt (am Beispiel):
fibonacci 6 -> (fibonacci 5) + (fibonacci 4)
Rekursionsanfang:
fibonacci 1 -> 1
fibonacci 2 -> 1
(c) Entwickle aus den Reduktionsregeln eine Funktionsdefinition für die Funktion fibonacci und teste sie in der REPL.
Quellen
- [1]: Kaninchenvermehrung - Urheber: Romain - Lizenz: Creative Commons BY-SA 4.0