Fachkonzept
Übersicht zu Syntaxdiagrammen
Im vorherigen Abschnitt hast du Syntaxdiagramme kennengelernt, die eine formale Sprache für (vereinfachte) E-Mail-Adresse definiert haben. Allgemein kann man Syntaxdiagramme wie folgt beschreiben.
Ein Syntaxdiagramm ist eine graphische Darstellung für Bildungsregeln von Texten. Damit definieren Syntaxdiagramme eine formale Sprache. Zu dieser Sprache gehören alle Zeichenfolgen, die nach den vorgegebenen Syntaxdiagrammen aufgebaut sind.
Ein Syntaxdiagramm besteht aus Terminalsymbolen, die in abgerundeten Elementen stehen, und Nichtterminalsymbolen, die in Rechtecken notiert sind. Die Terminalsymbole sind die Zeichen, die letztendlich im Text vorkommen müssen, die Nichtterminalsymbole müssen durch weitere Syntaxdiagramme definiert werden.
Ein Syntaxdiagramm hat immer einen Startpunkt und einen Endpunkt. Alle Wege vom Start zum Ende sind erlaubte Möglichkeiten, um einen Text zu bilden. Durch verschiedene Verbindungspfeile ergeben sich viele Optionen zur Sprachbeschreibung.
Die Diagramme enthalten verschiedene Elemente, die hier systematisch aufgelistet und mit entsprechenden Metazeichen von regulären Ausdrücken verglichen werden.
| Beispiel | Bedeutung | regulärer Ausdruck |
|---|---|---|
 |
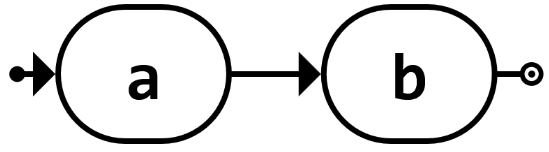Sequenz von Zeichen | ab |
 |
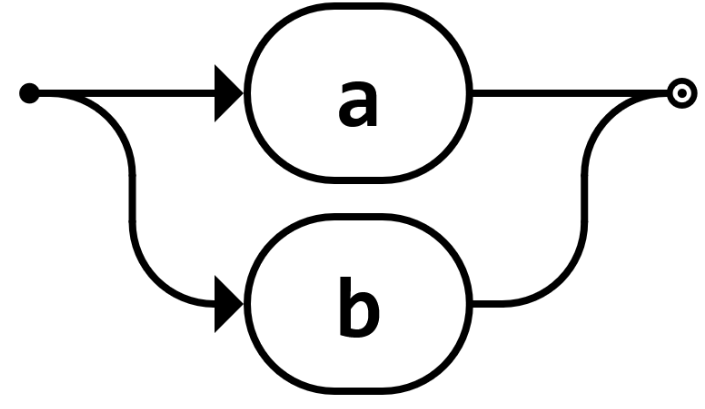Alternative von Zeichen | a|b |
 |
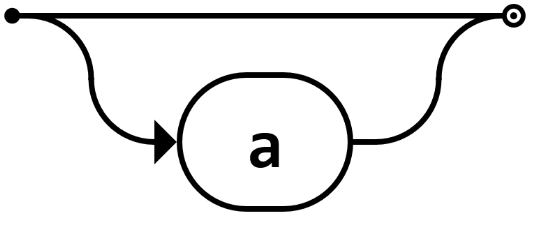Option für Zeichen | a? |
 |
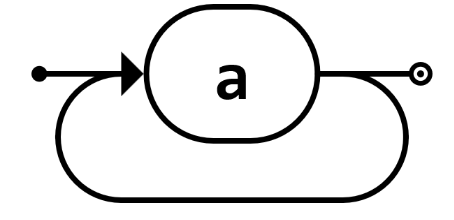mindestens eine Wiederholung | a+ |
 |
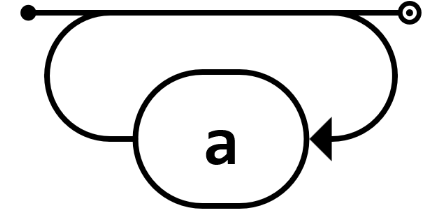beliebig viele (auch keine) Wiederholungen | a* |
 |
Nichterminalsymbol, "Aufruf" eines weiteren Syntaxdiagramms | Ähnlichkeit zu () |
 |
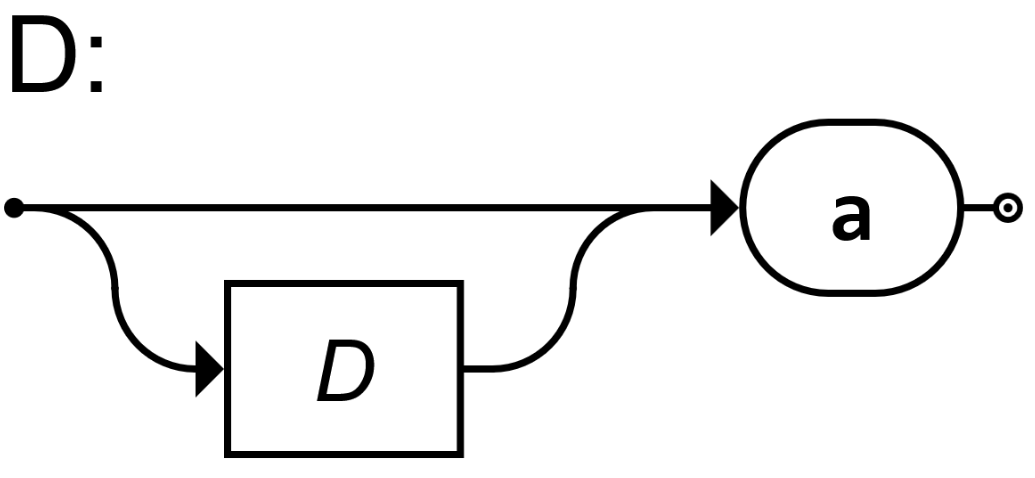rekursiver Aufruf des Diagramms D | keine Entsprechung |
Vertiefung
Durch die Möglichkeit, Sprachkonstrukte auch rekursiv zu definieren, kann man mit Syntaxdiagrammen auch nicht reguläre formale Sprachen beschreiben.
Das Syntaxdiagramm für die nicht reguläre Sprache anan, für die es keinen regulären Ausdruck gibt (!), sieht etwa wie folgt aus:
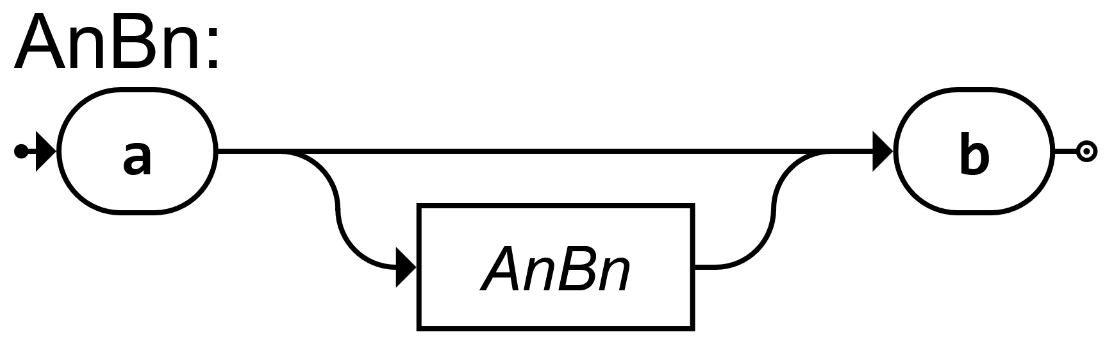Diese formale Sprache gehört zur Gruppe der kontextfreien Sprachen.
Mit Syntaxdiagrammen können zusätzlich zu den regulären Sprachen auch alle kontextfreien Sprachen definiert werden.
