Fachkonzept
Der erkennende endliche Automat (Akzeptor)
Aufgabe eines Akzeptors
Ein Akzeptor ist ein endlicher Automat, der die Syntaxprüfung für eine formale Sprache durchführen kann. Er bekommt zu Beginn ein Wort auf sein Eingabeband geschrieben und kann am Ende entscheiden, ob das eingegebene Wort syntaktisch korrekt aufgebaut ist und demnach zur definierten Sprache gehört.
Die Menge aller Wörter, die der Automat akzeptiert bildet die Sprache des Akzeptors. Es ist also auch möglich, eine Sprache mit einem Akzeptor zu definieren!
to+r) hast du einen Akzeptor kennen gelernt, der für jedes Eingabewort entscheiden konnte, ob es ein syntaktisch korrekter Torjubel ist. Die Sprache des Akzeptors war somit die Sprache der Torjubel.
Elemente eines Akzeptors
Ein erkennender endlicher Automat bzw. ein Akzeptor ist eine Verarbeitungseinheit, die durch folgende Bestandteile festgelegt wird:
- Die Zustandsmenge: eine nichtleere, endlichen Menge
Zvon Zuständen des Automaten. - Das Eingabealphabet: eine nichtleere, endlichen Menge
Evon Eingabesymbolen, aus denen Eingabeworte gebildet werden können. - Die Überführungsfunktion: eine Funktion, der Form f : Z x E -> Z, die jedem Paar aus aktuellem Zustand und Eingabe einen Folgezustand zuordnet. Die Überführungsfunktion wird entweder durch den Zustandsgraphen des Automaten oder durch eine Automatentafel definiert.
- Der Startzustand: ein ausgezeichnetes Element Z0 aus der Zustandsmenge.
- Die Endzustände: eine (in der Regel nicht-leere) Teilmenge Ze der Zustandsmenge.
Hierfür schreibt man auch kurz A = (Z, E, f, Z0, Ze).
to+r) besteht der Akzeptor entsprechend aus den folgenden Bestandteilen:
- Zustandsmenge Z = {Z0, Z1, Z2, Z3, Z4}
- Eingabealphabet E = {o,r,t}
- Startzustand Z0
- Endzustände Ze = {Z3}
- Überführungsfunktion: die folgenden Abbildungen zeigen beide Varianten zur Darstellung einer Überführungsfunktion: Die Automatentafel und den Zustandsgraphen. Als Beispiel ist die rot markierte Kante des Zustandsgraphen in der Automatentafel ebenfalls rot hinterlegt.
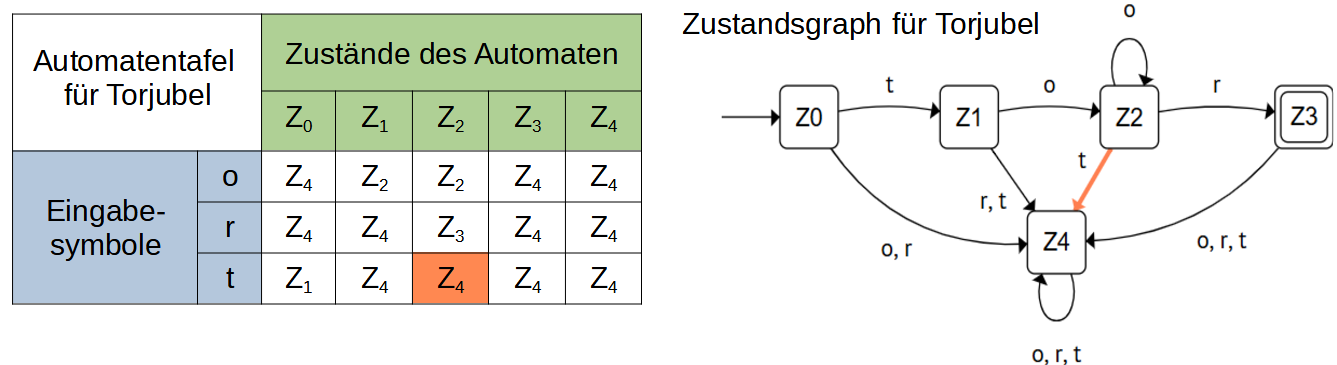Beide Varianten definieren dort (rot markiert) für die Überführungsfunktion an der Stelle Z=Z2 und E=t den Funktionswert Z4. Sprich: Wenn ich im Zustand Z2 ein t einlese, so gelange ich den in Zustand Z4.
Arbeitsweise eines Akzeptors
Ein Akzeptor arbeitet nach fest vorgegebenen Schritten:
- Startkonfiguration: Der Akzeptor befindet sich zu Beginn im Startzustand Z0. Das zu prüfende Wort steht auf dem Eingabeband des Akzeptors. Es wurde noch kein Eingabesymbol eingelesen. Der "Lesekopf" befindet sich somit auf dem ersten Zeichen des Eingabeworts.
-
Schrittweises Verarbeiten der Eingabezeichen:
- Symbol am Lesekopf einlesen
- Lesekopf um eine Stelle nach rechts verschieben
- In den Folgezustand wechseln (in Abhängigkeit vom aktuellen Zustand und des eingelesenen Symbols)
- Verarbeitungsende: der Akzeptor stoppt seine Arbeit, wenn das Eingabewort komplett abgearbeitet ist und kein Symbol mehr eingelesen werden kann. Der Lesekopf steht dann hinter dem letzten Eingabesymbol.
- Ergebnisermittlung: befindet sich der Automat am Ende in einem Endzustand aus Ze, so gilt das Eingabewort als akzeptiert.
Vertiefung
Das hier beschriebene Automatenmodell wird auch als deterministischer endlicher Automat (DEA) bezeichnet.
Der Automat heißt deterministisch, weil er für jeden Zustand und für jede Eingabe nur einen möglichen Folgezustand besitzt. Man kann auch Automaten konstruieren, bei denen von einem Zustand mehrere Übergänge mit dem selben Eingabezeichen abzweigen. Dann würde man von einem nichtdeterministischen Automaten sprechen. Diese Unterscheidung spielt für die Spracherkennung hier jedoch keine Rolle.
Der Automat heißt endlich, weil seine Zustandsmenge endlich ist. Du kannst dem Automat nicht unendlich viele Zustände hinzufügen. Deshalb kann ein Akzeptor z.B. auch irgendwann nicht mehr "mitzählen", wie viele Zeichen schon eingelesen wurden.
Ein DEA als Akzeptor kann nur reguläre Sprachen erkennen. Allerdings gibt es für jede reguläre Sprache einen Akzeptor.
Somit lässt sich sagen: Die Klasse der regulären Sprachen und die Klasse der mit einem Akzeptor definierbaren Sprachen sind identisch.
