Station - Verfahren mit modularer Potenz
Potenzbildung statt Addition und Multiplikation
Sowohl modulare Addition als auch modulare Multiplikation können als Grundlage eines Verfahrens zum Ver- und Entschlüsseln von Texten benutzt werden. Die resultierenden Verfahren sind jedoch ungeeignet für die Praxis, da sie unsicher sind.
Die nächste Stufe in der Hierarchie der Rechenoperationen nach Addition und Multiplikation stellt die modulare Potenzbildung dar.
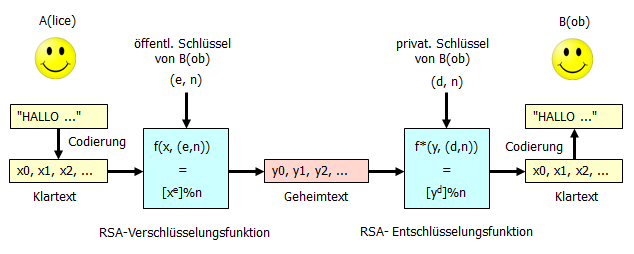
Im Folgenden soll erst einmal am Beispiel untersucht werden, ob sich auch diese Rechenoperation zum Ver- und Entschlüsseln von Texten eignet.

Wir gehen völlig analog zu den Verfahren mit modularer Addition und modularer Multiplikation vor. Als zentrale Rechenoperation nutzen wir hier die Potenzbildung. Beachte, dass die Potenz ab hier in der Form a**b dargestellt wird.
Wie man auf die beiden Schlüssel kommt, soll erst einmal zurückgestellt werden.
Aufgabe 1
(a) Rechne erst einmal die gezeigten Ergebnisse nach. Du kannst Python hier als Taschenrechner
benutzen.
>>> (19 ** 13) % 77 61
(b) Vervollständige die oben in der Übersicht gezeigte Ver- und Entschlüsselung.
Aufgabe 2
Führe das Verfahren mit modularer Potenz auch mit folgenden Daten durch. Welche Schwierigkeit tritt dabei auf?
(a)
Quelltext: ASTERIX Codierung: wie oben Blocklänge: 3 öffentlicher Schlüssel: (2008675, 2548873) privater Schlüssel: (377911, 2548873)
(b)
Quelltext: ASTERIX Codierung: wie oben Blocklänge: 4 öffentlicher Schlüssel: (377911777, 1919016703) privater Schlüssel: (626738065, 1919016703)

