Station - Sicherheit des Verfahrens
Angriffsszenario
Die folgende Übersicht verdeutlicht ein Angriffszenario auf eine mit dem RSA-Verfahren verschlüsselte Nachricht.
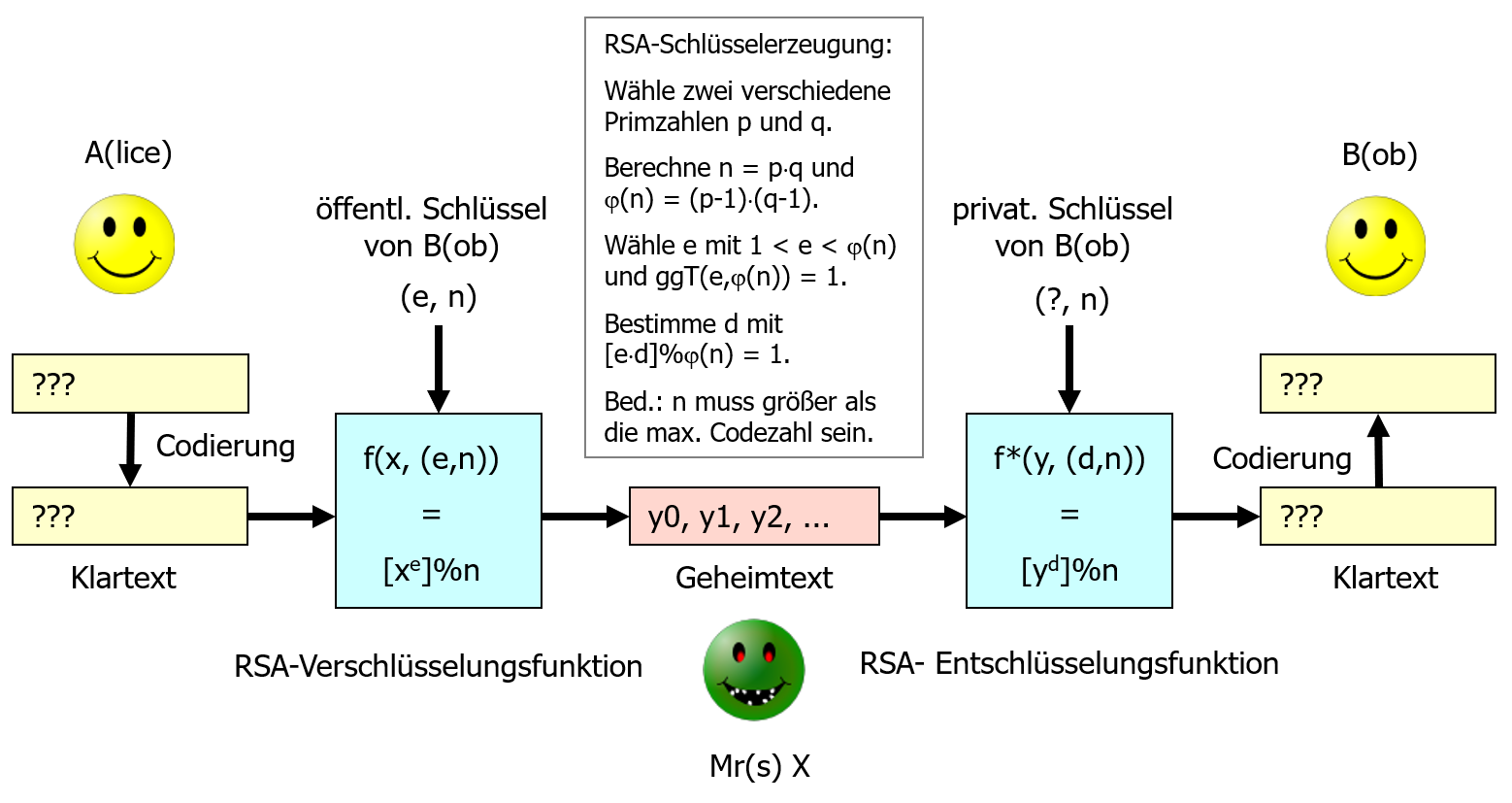
Mr(s). X verfügt neben dem abgefangenen Geheimtext (Sequenz von Zahlen) über eine Reihe weiterer Informationen. Er/Sie kennt den öffentlichen Schlüssel, der zum Verschlüsseln benutzt wurde. Er/Sie kennt zudem alle Details des RSA-Verfahrens: benutzte Codierung, Verfahren zur Erzeugung der Schlüssel, Verfahren zum Ver- und Entschlüsseln mit modularer Potenzbildung.
Aufgabe 1
Der öffentliche Schlüssel von Alice ist (19, 65). Es wurde unsere Standardcodierung mit einer Blocklänge 1 benutzt. Mr(s). X hat folgenden Geheimcode abgefangen:
[48, 9, 60, 38, 60, 0, 58, 47, 31, 60, 59, 59, 60, 0, 1, 31, 59, 0, 58, 1, 38, 38, 9, 60, 14]
Kannst du Mr(s). X helfen, die Nachricht zu entschlüsseln?
Aufgabe 2
Der öffentliche Schlüssel von Alice ist (113, 6887). Es wurde unsere Standardcodierung mit der Blocklänge 2 benutzt. Mr(s). X hat folgenden Geheimcode abgefangen:
[6613, 5456, 1378, 2773, 1646, 5581, 4072]
Kannst du Mr(s). X helfen, die Nachricht zu entschlüsseln? Wo liegt jetzt das Problem?
Aufgabe 3
Der öffentliche Schlüssel von Alice ist (1432765433173537777777, 1914269284601333234385791628203). Es wurde unsere Standardcodierung mit der Blocklänge 15 benutzt. Mr(s). X hat folgenden Geheimcode abgefangen:
[1484723618683282017476932691981, 1335981139459882474539235587779]
Kannst du Mr(s). X helfen, die Nachricht zu entschlüsseln? Wo liegt jetzt das Problem?
Angriff auf das RSA-Verfahren

Wenn Mr(s). X über den privaten Schlüssel (d, n) verfügt, kann er/sie den Geheimtext entschlüsseln.
Da n aus dem öffentlichen Schlüssel bekannt ist, muss Mr(s). X nur
noch d bestimmen.
Aufgabe 4
Erkläre anhand der Aufgaben 1 bis 3, welche Schritte Mr(s). X unternehmen muss, um d zu bestimmen.
🔑 Lösung
Mr(s). X weiß, dass n das Produkt aus zwei verschiedenen Primzahlen ist. Mr(s). X zerlegt also n in ein Produkt p*q mit den beiden Primzahlen p und q.
Beispiel (Aufgabe 1): n = 65 -> p = 5 und q = 13
Aus den beiden Primzahlen p und q kann Mr(s). X die Zahl φ(n) = (p-1) * (q-1) berechnen.
Beispiel (Aufgabe 1): p = 5 und q = 13 -> φ(n) = 48
Mr(s). X weiß zudem, dass die Zahl d modulares Inverses von e bzgl. φ(n) ist bzw., dass [e*d]%φ(n) = 1 gilt. Mit dem erweiterten euklidischen Algorithmus kann Mr(s). X diese Zahl d bestimmen.
Beispiel (Aufgabe 1): e = 19 und φ(n) = 48: [19*d]%48 = 1 -> d = 43
Mr(s). X kennt jetzt den privaten Schlüssel und kann den Geheimtext entschlüsseln.
Sicherheit des RSA-Verfahrens

Die Sicherheit beruht darauf, ob Mr(s). X aus dem öffentlichen Schlüssel (e, n) den privaten Schlüssel (d, n) berechnen kann.
Aufgabe 5
(a) Erkläre, dass eine solche Berechnung immer möglich ist.
(b) Begründe, dass die Sicherheit des RSA-Verfahrens nur davon abhängt, wie schnell man die Zahl n in ihre beiden Faktoren p und q zerlegen kann. (Das nennt man die Faktorisierung von n.)
(c) Welche Zeitspanne zur Faktorisierung (und damit zum Knacken des RSA-Verfahrens) ist in deinen Augen angemessen, um von einem sicheren Verfahren sprechen zu können?
Eine Einwegfunktion
In Aufgabe 5 wurde herausgearbeitet, dass die Faktorisierung von n der essentielle Schritt beim Knacken des RSA-Verfahrens darstellt. Das Faktorisieren ist dabei das Gegenteil der Multiplikation: Faktorisierung bedeutet, n in p und q zu zerlegen; Multiplizieren bedeutet, aus p und q das Produkt n zu berechnen.
Aufgabe 6
(a) Beschreibe, wo im RSA-Verfahren die Multiplikation von p und q benötigt wird.
(b) Für die Anwendbarkeit des RSA-Verfahrens fordert man, dass auf der einen Seite diese Multiplikation in sinnvoller Zeit lösbar sein muss, während die Faktorisierung möglichst lange dauern muss. Erkläre den ersten Teil der Forderung.
(c) Eine Funktion, die die Forderung aus (b) erfüllt, nennt man Einwegfunktion. Erkläre den Begriff.
(d) Experimentiere mit dem folgenden Tool und untersuche dabei, ob die Multiplikation zweier Primzahlen eine Einwegfunktion darstellt.
(e) Erläutere, warum diese Experimente nicht ausreichen, um definitiv zu sagen, dass eine Einwegfunktion gefunden wurde (und damit das RSA-Verfahren als sicher angesehen werden kann).
💡 Tipp
Wiederhole die Überlegungen der Verschlüsselung mit modularer Multiplikation. Dabei sah es erst so aus, als wäre ein sicheres Verfahren gefunden worden.
Im nächsten Abschnitt wird das Faktorisierungsproblem genauer untersucht.

