Station - Modulare Addition
Rechnen mit Uhrzeiten
Hier noch einmal der Fahrplan der Transsibirischen Eisenbahn:
| Station | Fahrzeit [h] | Uhrzeit [MOZ] | Rechnung |
|---|---|---|---|
| MOSKVA | 17:00 | ||
| KIROV | 12 | 05:00 | [17 + 12]%24 = 5 |
| EKATERINBURG | 26 | 19:00 | [17 + 26]%24 = [43]%24 = 19 |
| NOVOSIBIRSK | 46 | ||
| KRASNOYARSK | 58 | ||
| IRKUTSK | 77 | ||
| BIROBIDJAN | 133 | ||
| VLADIVOSTOK | 149 |
Aufgabe 1
(a) Führe die Rechnung für weitere Städte durch.
(b) Darf man für EKATERINBURG auch so rechnen:
[17 + 26]%24 = [17]%24 + [26]%24 = ...(c) Geht das auch für NOVOSIBIRSK? Was müsste man hier noch tun?
[17 + 46]%24 = [17]%24 + [46]%24 = ...
Addition modulo einer vorgegebenen Zahl
Vorgegeben sei eine natürliche Zahl n. Zwei natürliche Zahlen a und b werden modulo n addiert, indem man sie addiert und anschließend von der Summe den Rest bei der Division durch n berechnet. Das Ergebnis ist also [a+b]%n. Beachte, dass das Ergebnis bei der Addition modulo n immer eine Zahl kleiner als n ist.
Die Addition modulo n lässt sich gut mit einer Verknüpfungstafel verdeutlichen. Im folgenden Beispiel ist n = 4 gewählt.
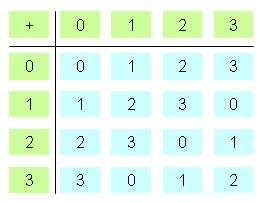
Aufgabe 2
Erstelle selbst eine Verknüpfungstafel für die Addition modulo n = 5.
Aufgabe 3
(a) Wie kann man aus einer Verknüpfungstafel zur Addition modulo n die Gegenzahl modulo n
zu einer
Zahl bestimmen? Wie erhält man beispielsweise bei n = 4 die Gegenzahl modulo 4 zur Zahl a = 3, d.h. die Zahl x mit
[3+x]%4 = 0?
(b) Warum gibt es bei gegebenem n zu jeder Zahl a eine solche additive Gegenzahl modulo n?
Rechengesetze für die Addition modulo n
Für die Addition modulo n gelten eine Reihe von Rechengesetze wie z.B. das Kommutativ- und das Assoziativgesetz. Wir benötigen zusätzlich die beiden folgenden Rechengesetze:
Modulare Gleichheit bei der Addition
Aus [a1]%n = [b1]%n und [a2]%n = [b2]%n folgt [a1+a2]%n = [b1+b2]%n.
Das erste Rechengesetz besagt, dass Zahlen, die modulo n gleich sind, auch zu gleichen Additionsergebnissen modulo n führen.
Addition und iterierte Modulberechnung
[a+b]%n = [[a]%n + [b]%n]%n
Das zweite Rechengesetz erlaubt es, bei der Addition modulo n zuerst die Summanden zu verkleinern und dann erst die Addition durchzuführen.
Aufgabe 4
Bestätige die Rechengesetze anhand von Beispielen. Du kannst Python als Taschenrechner benutzen.
>>> n = 14
>>> a1 = 16
>>> a2 = 19
>>> b1 = 44
>>> b2 = 75
>>> a1%n
2
>>> b1%n
2
>>> a2%n
5
>>> b2%n
5
>>> (a1+a2)%n
...
n = 14 a1 = 16 a2 = 19 b1 = 44 b2 = 75 print(a1%n)
Exkurs: Mathematik (Gruppen)
Die Gruppe $\mathbb{Z}_n$
Sei $n \in \mathbb{N}$ eine Modulo-Zahl. In der Mathematik definiert man für $a,b\in\mathbb{Z}$ sogenannte Restklassen $[a]$, $[b]$ durch: $$ [a]=[b] \quad \Leftrightarrow \quad a\%n = b\%n$$ a und b sind also verschiedene Repräsentanten der gleichen Restklasse.Mit $\mathbb{Z}_n$ bezeichnet man die Menge der Restklassen modulo n, verdeutlicht an einem Beispiel: $$\mathbb{Z}_5 = \{[0],[1],[2],[3],[4]\}$$ In $\mathbb{Z}_5$ sind $[2] = [7]$ zwei Repräsentanten der gleichen Restklasse, da $2\%5 = 7\%5$.
Die Menge $\mathbb{Z}_n$ bildet dann zusammmen mit der Operation + eine sogenannte Gruppe. Eine Gruppe wiederum ist eine Menge, in der eine Verknüpfung (hier +) definiert ist, die folgende Eigenschaften erfüllt:
- Assoziativgesetz: $([a]+[b])+[c] = [a]+([b]+[c]) = [a]+[b]+[c]$
- Neutrales Element: Es gibt ein neutrales Element $[0]$ mit $[a]+[0] = [0]+[a] = [a]$
- Inverses Element: Zu jedem Element $[a]$ gibt es ein Gegen-Element $[b]$ mit $[a]+[b] = [b]+[a] = [1]$
- Kommutativgesetz: $[a]+[b] = [b]+[a]$.
Im weiteren Verlauf des Kapitels werden wir diese Rechengesetze benötigen. Man kann sie sich aber leicht merken, da sie die gleichen sind wie bei den ganzen Zahlen $\mathbb{Z}$. Denn die ganzen Zahlen bilden bezüglich der Addition ebenfalls eine kommutative Gruppe.

