Station - Schnelles modulares Potenzieren
Schwierigkeiten beim Potenzieren
Beim Rechnen mit Potenzen erhält man große Zahlen als Ergebnisse:
>>> 24 ** 13
876488338465357824
>>> 876488338465357824 % 77
52
>>> 52 ** 37
3105444088679819357273546406651335246066988648897330641813635072
>>> 3105444088679819357273546406651335246066988648897330641813635072 % 77
24
Wenn die Ausgangszahlen jetzt ebenfalls groß sind, dann muss das Ausführsystem riesige Zahlen verwalten. Python liefert bei solch großen Zahlen erst einmal keine Ergebnisse.
>>> 11920 ** 2008675 ???
Um das Verfahren mit modularer Potenz mit großen Zahlen durchführen zu können, benötigt man Verfahren zur Berechnung von (modularen) Potenzen, die auch für große Zahlen schnell Ergebnisse liefern.
Schnelles Potenzieren
Wie berechnet man eine Potenz - z.B. die Potenz 316?
Potenzen berechnet man üblicherweise, indem man schrittweise die zu potenzierende Zahl mit einem Zwischenergebnis multipliziert.
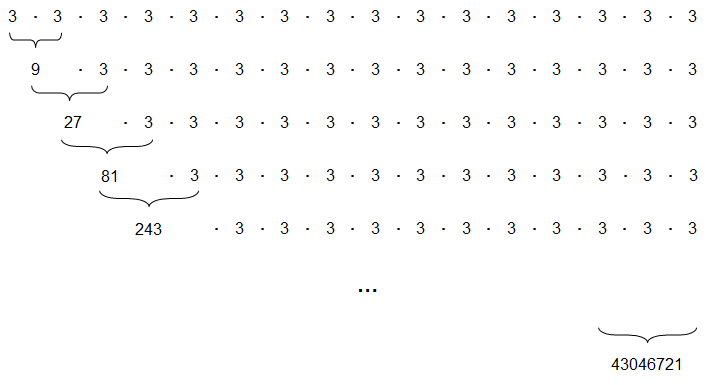
Bei einer Potenz mit einer Zweierpotenz als Exponenten - wie im Beispiel 316 - kann man aber auch anders vorgehen:
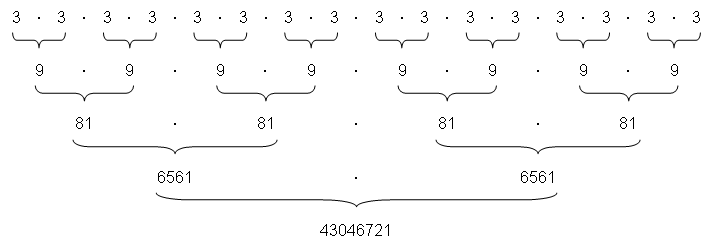
Das Berechnungsverfahren lässt sich gut in Tabellenform darstellen:
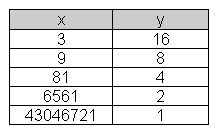
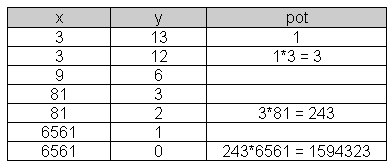
Das Verfahren bei Zweierpotenzen als Exponenten lässt sich auf beliebigen Exponenten übertragen. Man muss nur zusätzlich die Faktoren verwalten, die beim Quadrieren übrig bleiben. Die Abbildung zeigt die Berechnung von 313.
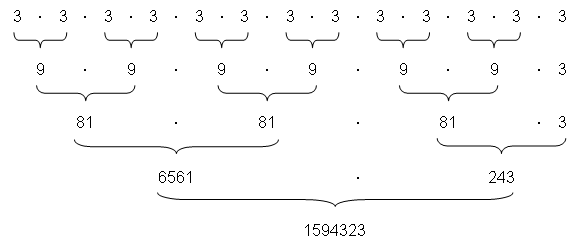
In Tabellenform sieht die Berechnung dann so aus:
Aufgabe 1
(a) Vergleiche zunächst die beiden Verfahren zur Berechnung der Potenz 316. Wie viele Rechenoperationen (Multiplikationen) werden beim Iterationsverfahren benötigt? Wie viele Rechenoperationen (Multiplikationen und Divisionen) werden beim Quadrierungsverfahren benötigt? Wie wiele Rechenoperationen werden jeweils zur Berechnung der Potenz 31024 benötigt? Warum ist das Quadrierungsverfahren effizienter?
(b) Analysiere das Quadierungsverfahren bei beliebigen Potenzen. Berechne analog die Potenzen 515 und 723. Kontrolliere jeweils die Ergebnisse.
(c) Vergleiche auch bei beliebigen Potenzen die Anzahl der erforderlichen Rechenoperationen beim Iterations- und Quadrierungsverfahren. Betrachte den ungünstigsten Fall.
Schnelles modulares Potenzieren
Beim modularen Potenzen kann man zuerst die Potenz berechnen und anschließend den modularen Rest.
[7 * 7 * 7]% 5 = [343]%5 = 3
Mit geigneten Rechengesetzen (siehe Station - Modulare Potenz). kann man die Modulbildung aber auch nach jedem Rechenschritt durchführen.
[7 * 7 * 7]% 5 = [[ [7]%5 * [7]%5 ]%5 * [7]%5 ] %5 = [[ 2 * 2 ]%5 * [7]%5 ] %5 = [[ 4 ]%5 * [7]%5 ] %5 = [ 4 * 2 ] %5 = [ 8 ] %5 = 3
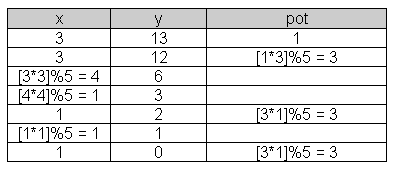
Entsprechend kann man modulares Potenzieren mit dem Quadrierungsverfahren durchführen. In der folgenden Tabelle ist die Berechnung von [313]%5 dargestellt.
Aufgabe 2
(a) Berechne analog die modularen Potenzen [517]%7 und [5237]%77. Kontrolliere jeweils die Ergebnisse.
(b) Wie groß werden die zu verwaltenden Zwischenergebnisse maximal bei der Berechnung einer modularen Potenz wie z.B. [5237]%77?
Algorithmen zum schnellen Potenzieren
Hier noch einmal die oben entwickelte Tabelle zur Berechnung der Potenz 313:

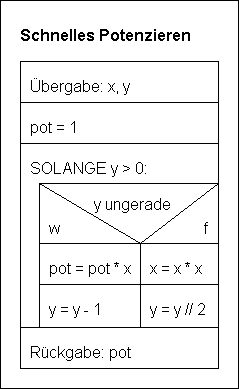
Das hier benutzte Quadrierungsverfahren lässt sich wie folgt als Algorithmus formulieren.
Analog geht man bei der Berechnung modularer Potenzen vor - wie die Tabelle zur Berechnung der Potenz [313]%5 zeigt:

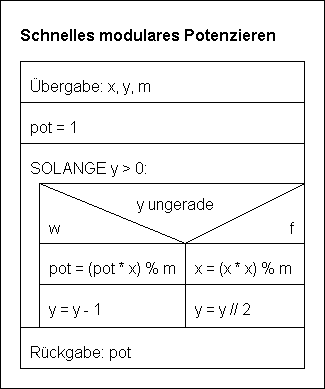
Hieraus ergibt sich der folgende Algorithmus:
Aufgabe 3
(a) Teste die folgende Implementierung des Algorithmus Schnelles Potenzieren
.
def pot(x, y):
pot = 1
while y > 0:
if y % 2 == 1:
pot = pot * x
y = y - 1
else:
x = x * x
y = y // 2
return pot
(b) Teste ebenfalls die folgende Implementierung des Algorithmus Schnelles modulares Potenzieren
.
Teste sie insbesondere mit großen Zahlen.
def modpot(x, y, m):
pot = 1
while y > 0:
if y % 2 == 1:
pot = (pot * x) % m
y = y - 1
else:
x = (x * x) % m
y = y // 2
return pot

