Station - Modulare Multiplikation
Multiplikation modulo einer vorgegebenen Zahl
Die Multiplikation modulo einer vorgegebenen Zahl wird analog zur Addition durchgeführt.
Vorgegeben sei eine natürliche Zahl n. Zwei natürliche Zahlen a und b werden modulo n multipliziert, indem man sie multipliziert und anschließend vom Produkt den Rest bei der Division durch n berechnet. Das Ergebnis ist also [a*b]%n. Beachte, dass das Ergebnis bei der Multiplikation modulo n immer eine Zahl kleiner als n ist.
Auch die Multiplikation modulo n lässt sich gut mit einer Verknüpfungstafel verdeutlichen. Im folgenden Beispiel ist n = 5 gewählt.
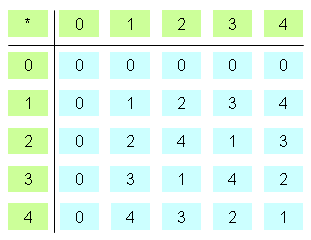
Aufgabe 1
Erstelle selbst eine Verknüpfungstafel für die Multiplikation modulo n = 8.
Rechengesetze für die Multiplikation modulo n
Für die Multiplikation modulo n gelten eine Reihe von Rechengesetze wie z.B. das Kommutativ- und das Assoziativgesetz. Wir benötigen zusätzlich die beiden folgenden Rechengesetze:
Modulare Gleichheit bei der Multiplikation
Aus [a1]%n = [a2]%n und [b1]%n = [b2]%n folgt [a1*b1]%n = [a2*b2]%n.
Das erste Rechengesetz besagt, dass Zahlen, die modulo n gleich sind, auch zu gleichen Multiplikationsergebnissen modulo n führen.
Multiplikation und iterierte Modulberechnung
[a*b]%n = [[a]%n * [b]%n]%n
Das zweite Rechengesetz erlaubt es, bei der Multiplikation modulo n zuerst die Faktoren zu verkleinern und dann erst die Multiplikation durchzuführen.
Aufgabe 2
Bestätige die Rechengesetze anhand von Beispielen. Du kannst Python als Taschenrechner benutzen.
>>> n = 14
>>> a1 = 16
>>> b1 = 19
>>> a2 = 44
>>> b2 = 75
>>> a1%n
2
>>> a2%n
2
>>> b1%n
5
>>> b2%n
5
>>> (a1*b1)%n
...
n = 14
a1 = 16
a2 = 19
b1 = 44
b2 = 75
print(a1%n)
Das modulare Inverse
Beim Umkehren von Rechenoperationen spielen sogenannte Inverse eine zentrale Rolle. So ist -4 das Inverse von +4 bzgl. der üblichen Addition bei ganzen Zahlen. Ebenso ist 1/2 das Inverse von 2 bzgl. der üblichen Multiplikation bei rationalen Zahlen.
Beim RSA-Verfahren spielt das Inverse bei der modularen Multiplikation eine wichtige Rolle. Dieses Inverse wird auch modulares Inverse genannt.
Zwei natürliche Zahlen a und b heißen modular invers zueinander bezüglich n genau dann, wenn gilt: [a*b]%n = 1.
Beispiel: Es gilt [2*3]%5 = 1. Die beiden Zahlen 2 und 3 sind also modular invers zueinander bzgl. 5. Die Zahl 2 ist das modulare Inverse von 3 bzgl. des Moduls 5. Ebenso ist 3 das modulare Inverse von 2 bzgl. des Moduls 5.
Aufgabe 3
(a) Betrachte den Fall n = 5 (siehe Verknüpfungstafel oben). Bestimme zu a = 1, 2, 3, 4 jeweils das modulare Inverse bzgl. n.
(b) Betrachte den Fall n = 8 (siehe Aufgabe 1). Für welche der Zahlen a = 1, 2, ..., 7 kann man das modulare Inverse bzgl. n bestimmen?
(c) Betrachte den Fall n = 15. Hast du bereits eine Vermutung, für welche der Zahlen a = 1, 2, ..., 14 man das modulare Inverse bzgl. n bestimmen kann?
Satz (über die Existenz des modularen Inversen)
Gegeben sei eine natürliche Zahl n. Das modulare Inverse bezüglich n zu einer Zahl a ungleich Null existiert genau dann, wenn a und n keinen gemeinsamen Teiler größer als 1 haben - d.h., wenn ggT(a, n) = 1 gilt.
Den allgemeinen Beweis dieser Aussage findest du im späteren Abschnitt Station - Berechnung der modularen Inversen. Dort wird erklärt, wie die modulare Inverse mithilfe des erweiterten euklidischen Algorithmus berechnet werden kann.
Aufgabe 4
Entwickle eine Python-Funktion modInv(a, n), die das modulare Inverse von a bzgl. n
zurückgibt, sofern dieses Inverse existiert. Wenn keine solche Zahl existiert, soll der Wert -1
zurückgegeben werden.
Tipp: Man kann der Reihe nach alle in Frage kommenden Zahlen durchprobieren.
Exkurs: Mathematik (Halbgruppen, Ringe, Körper)
Die multiplikative Halbgruppe $\mathbb{Z}_n$
Im Exkurs des letzten Abschnitte haben wir die additive kommutative Gruppe $\mathbb{Z}_n$ der Restklassen modulo n kennengelernt.Die Menge $\mathbb{Z}_n$ der Restklassen modulo n ist eine sogenannte Halbgruppe bezüglich der Multiplikation. Das bedeutet, dass die Multiplikation auf $\mathbb{Z}_n$ die folgenden Eigenschaften erfüllt:
- Assoziativgesetz: $([a]*[b])*[c] = [a]*([b]*[c]) = [a]*[b]*[c]$
- Neutrales Element: Es gibt ein neutrales Element $[1]$ mit $[a]*[1] = [1]*[a] = [a]$
Falls die Modulo-Zahl jedoch eine Primzahl $p$ ist, dann ist $\mathbb{Z}_p$ sogar eine Gruppe bezüglich der Multiplikation.
Restklassenring $\mathbb{Z}_n$
Die Menge $\mathbb{Z}_n$ der Restklassen modulo n bildet zusammen mit der Addition und der Multiplikation einen sogenannten Restklassenring, dh. es gelten die Rechengesetze der Addition und Multiplikation, die wir von den ganzen Zahlen $\mathbb{Z}$ kennen. Zu den Rechengesetzen der Gruppe bzw. Halbgruppe kommt also noch das Distributivgesetz, das die Multiplikation und Addition miteinander verknüpft.Im weiteren Verlauf des Kapitel benötigen wir all diese Rechengesetze, allerdings wird uns das nicht sonderlich schwerfallen, da sie die gleichen sind wie bei den ganzen Zahlen $\mathbb{Z}$. Denn die ganzen Zahlen bilden bezüglich der Addition und Multiplikation ebenfalls einen Ring. (Allerdings sind die Rechengesetze für $\mathbb{Z}_n$ eigentlich noch beweisbedürftig, was wir aber hier nicht weiter ausführen.)

