Implementierung einer Nachbarschaftstabelle
Implementierung mit Listen
Wir betrachten weiterhin den folgenden Graphen:
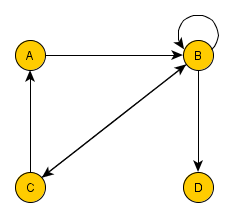
Die Nachbarschaftstabelle zu diesem Graphen lässt sich in Python mit Hilfevon Listen nachbilden.
knotenliste = ['A', 'B', 'C', 'D'] adjazenzmatrix = [[0, 1, 0, 0], [0, 1, 1, 1], [1, 1, 0, 0], [0, 0, 0, 0]]
Aufgabe 1
(a) (einfach)
Entwickle eine Funktion existiertKnoten(nameKnoten), die
überprüft, ob ein vorgegebener Knoten im Graph vorkommt.
Teste das Verhalten der Funktion, z.B. so:
>>> knotenliste = ['A', 'B', 'C', 'D']
>>> adjazenzmatrix = [[0, 1, 0, 0], [0, 1, 1, 1], [1, 1, 0, 0], [0, 0, 0, 0]]
>>> existiertKnoten('D')
True
>>> existiertKnoten('G')
False
(b) (etwas schwieriger)
Entwickle eine Funktion existiertKante(nameStartKnoten, nameZielKnoten), die überprüft,
ob es eine Kante zwischen den übergebenen Knoten gibt.
Teste das Verhalten der Funktion, z.B. so:
>>> knotenliste = ['A', 'B', 'C', 'D']
>>> adjazenzmatrix = [[0, 1, 0, 0], [0, 1, 1, 1], [1, 1, 0, 0], [0, 0, 0, 0]]
>>> existiertKante('A', 'D')
False
>>> existiertKante('B', 'D')
True
>>> existiertKante('X', 'Y')
False
Tipp: Mit knotenliste.index('A') kann man den Index des übergebenen Bezeichners in
der Knotenliste bestimmen.
(c) (noch etwas schwieriger)
Entwickle eine Funktion getAlleNachbarn(nameKnoten), die sämtliche Nachbarn eines vorgegebenen
Knotens ermittelt und zurückgibt.
>>> knotenliste = ['A', 'B', 'C', 'D']
>>> adjazenzmatrix = [[0, 1, 0, 0], [0, 1, 1, 1], [1, 1, 0, 0], [0, 0, 0, 0]]
>>> getAlleNachbarn('B')
['B', 'C', 'D']
Objektorientierte Modellierung
Für die weitere Verarbeitung von Graphen ist es günstig, Graphen als Objekte
einer Klasse Graph zu realisieren.

Aufgabe 2
(a) Überlege dir, welche Operationen ein Graph-Objekt ausführen können soll.
Einige Operationen werden bereits in Aufgabe 1 thematisiert.
Erstelle ein Klassendiagramm zur Dokumentation der Klasse.
(b) Implementiere die Klasse Graph. Teste die Implementierung mit einem
geeigneten Python-Dialog oder einem einfachen Testprogramm.

