Der Algorithmus von Dijkstra
Minimale Abstände und kürzeste Wege in gewichteten Graphen
In gewichteten Graphen wird üblicherweise der Abstand zwischen zwei Knoten über die Gewichte der Kanten festgelegt. Der Abstand zweier Knoten längs eines Weges ergibt sich als Summe der Gewichte der Kanten, die den Weg bilden.
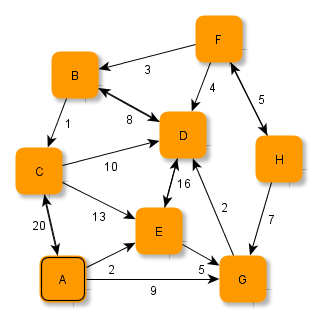
Die Bestimmung minimaler Abstände und kürzester Wege kann ähnlich zu dem Verfahren des letzten Abschnitts erfolgen.
Aufgabe 1
Die Abbildungen zeigen ein Verfahren, wie man systematisch minimale Abstände und kürzeste in einem gewichteten Graphen ermitteln kann.
Versuche, anhand der Abbildungen das Verfahren zu erschließen und folgende Fragen zu klären: Welche Knoten werden jeweils grün / blau markiert? Wie werden die zu verarbeitenden Knoten ausgewählt? Wie kommen die Zahlen (als Zusatzinformationen an den Knoten) zustande? Warum müssen Zahlen manchmal auch abgeändert werden? Warum hört das Verfahren nach der letzten Abbildung auf? Wie ist das Ergebnis zu deuten?

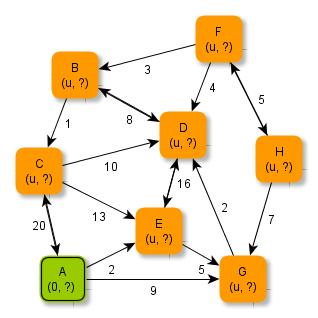
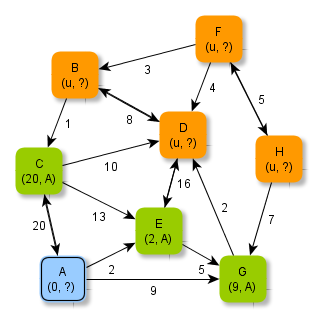
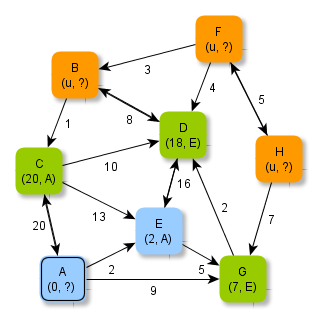
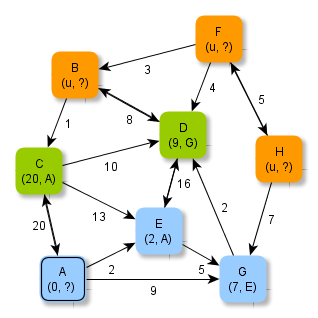
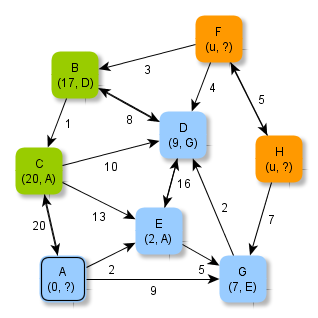
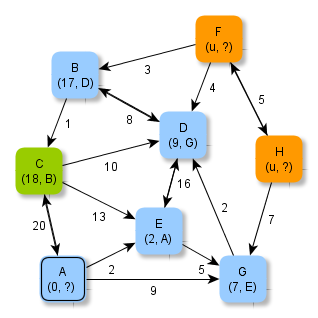
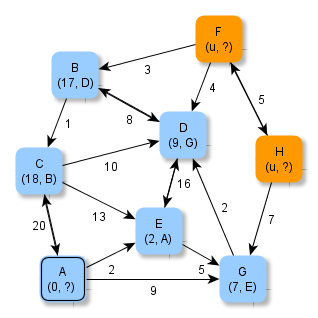
Der Algorithmus zum Verfahren - Algorithmus von Dijkstra
Das Verfahren zur Bestimmung kürzester Wege in gewichteten Graphen verarbeitet Graphen ähnlich wie der Algorithmus von Moore. Genau wie beim Algorithmus von Moore wird der Graph in einem ersten Schritt vorbereitet:

Jeder Knoten wird mit Zusatzinformation versehen, die den aktuellen Kenntnisstand über Abstand und Herkunft eines kürzesten Weges beschreiben.

Die eigentliche Verarbeitung erfolgt ähnlich wie beim Algorithmus von Moore:

Bei der Wahl des nächsten zu verarbeitenden Knotens wird hier der Knoten aus der Liste (grün) ausgewählt, der bis zu diesem Verarbeitungsschritt einen minimalen Abstand zum Startknoten aufweist. Im vorliegenden Fall ist das der Knoten E. Von diesem Knoten aus werden alle noch nicht verarbeiteten Nachbarknoten berücksichtigt (hier D und G). Wenn diese noch nicht in der Liste der noch zu verarbeitenden Knoten liegen (wie D), dann werden die Zusatzinformationen neu gesetzt. Wenn sie bereits in der Liste der noch zu verarbeitenden Knoten vorkommen (wie G), dann wird überprüft, ob es einen kürzeren Weg über den ausgewählten Knoten gibt. Im vorliegenden Fall ist der Weg vom Startknoten A zum Knoten G über den Knoten E kürzer als direkte Weg von A nach G. Daher werden hier die Zusatzinformationen entsprechend abgeändert.

Dieses Verfahren bildet die Grundlage des Algorithmus von Dijkstra:
ALGORITHMUS # von Dijkstra
Übergabedaten: Graph, startKnoten, zielKnoten
# Vorbereitung des Graphen
für alle knoten des Graphen:
setze abstand auf 'u'
setze herkunft auf None
setze abstand von startKnoten.abstand auf 0
füge startKnoten in eine Liste zuVerarbeiten ein
# Verarbeitung der Knoten
SOLANGE die Liste zuVerarbeiten nicht leer ist:
bestimme einen Knoten minKnoten aus zuVerarbeiten mit minimalem Abstand
entferne minKnoten aus zuVerarbeiten
für alle nachbarKnoten von minKnoten:
gewicht = Gewicht der Kante von minKnoten zu nachbarKnoten
neuerAbstand = (abstand von minKnoten) + gewicht
WENN abstand von nachbarKnoten == 'u':
füge nachbarKnoten in die Liste zuVerarbeiten ein (z.B. am Listenende)
setze abstand von nachbarKnoten auf neuerAbstand
setze herkunft von nachbarKnoten auf minKnoten
SONST:
WENN nachbarKnoten in zuVerarbeiten liegt:
WENN abstand von nachbarKnoten > neuerAbstand:
setze abstand von nachbarKnoten auf neuerAbstand
setze herkunft von nachbarKnoten auf minKnoten
weglaenge = abstand von zielKnoten
# Erzeugung des Weges zum zielKnoten
weg = []
knoten = zielKnoten
SOLANGE knoten != startKnoten und herkunft von knoten != None:
weg = [(herkunft von knoten, knoten)] + weg
knoten = herkunft von knoten
Rückgabedaten: (weg, weglaenge)
Aufgabe 2
Führe den Algorithmus mit F als Startknoten aus. Als Hilfe kannst du dir ein Arbeitsblatt mit leeren Graphen ausdrucken.

