Exkurs - Graphen in Anwendungssituationen
Vorbemerkung
Es gibt eine riesige Vielfalt an Situationen, die man mit Graphen adäquat beschreiben kann. Im Folgenden können nur wenige solcher Situationen erfasst werden. Du kannst ja selbst versuchen, weitere Anwendungsmöglichkeiten zu finden.
Fährverbindungen in der Ostsee
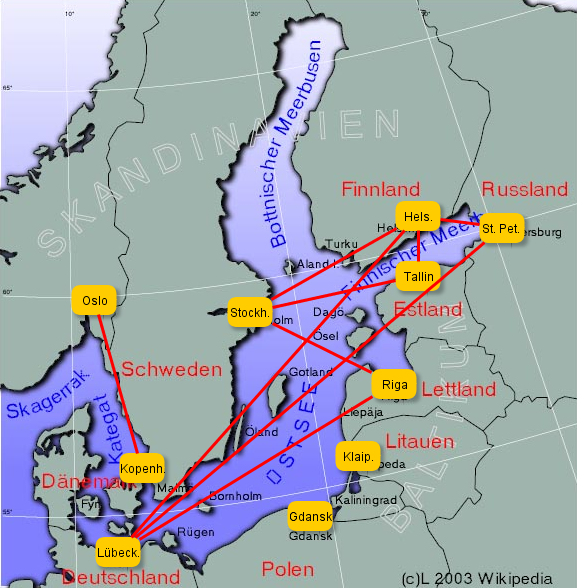
Wenn man eine Reise nach Finnland mit einer Fähre plant, muss man sich über die Fährverbindungen in der Ostsee informieren. Die folgende Karte zeigt wichtige Fährhäfen und die Fährverbindungen zwischen diesen Fährhäfen. Beachte, dass es eine Reihe weiterer Fährhäfen und Fährverbindungen gibt (siehe z.B. Ferrycenter).
Aufgabe 1
(a) Wie sind die Verbindungslinien zwischen den Fährhäfen hier zu deuten? Warum beschreiben sie nicht die tatsächlichen Schifffahrsrouten? Warum reicht hier eine abstrahierende Darstellung der Fährverbindungen?
(b) Man möchte zusätzlich die Streckenlängen der Fährverbindungen angeben. Wie könnte man solche Informationen in der gezeigten Darstellung integrieren?
Länder und ihre Nachbarn
Wie kommt man über Land von Deutschland nach Finnland? Wie viele Ländergrenzen muss man dabei mindestens passieren?
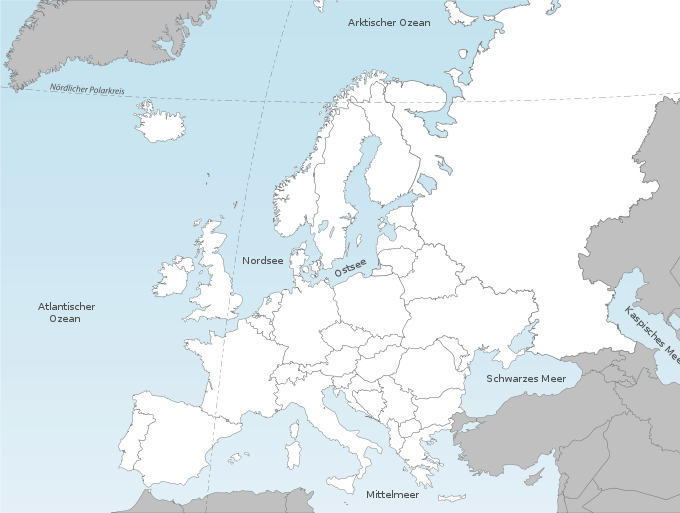
Das Problem lässt sich leicht mit der gezeigten Europakarte lösen (sofern man weiß, wo Deuschland und Finnland liegen).
Das Problem lässt sich ebenfalls lösen, wenn man benachbarte Länder in einem Graphen mit Knoten und Kanten darstellt:
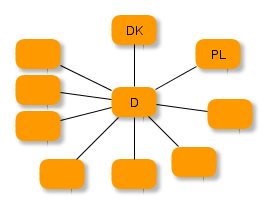
Aufgabe 2
(a) Der (noch unfertige Graph) zeigt Deutschland und seine Nachbarländer. Trage erst einmal sämtliche noch fehlenden Nachbarländer in die bereits vorgegebenen Knoten ein.
(b) Wie würde man die Kanten in der gezeigten Darstellung deuten?
(c) Erweitere das Diagramm um die Nachbarländer von Polen usw., bis du das oben beschriebene Problem mit Hilfe des Graphen lösen kannst.
(d) Wie kommt man über Land von Finnland nach Irland? Wie würde man das am Graphen erkennen?
Brücken verbinden Stadtteile
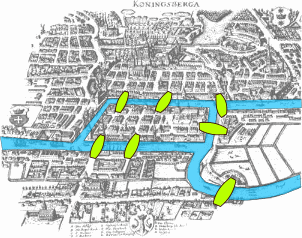
In Königsberg (heute Kaliningrad) teilt der Fluss Pregel die Stadt in mehrere Stadtteile auf. Der Stadtplan hebt die Brücken hervor, die die Stadtteile miteinander verbinden.
Der Mathematiker Euler beschäftigte sich mit der Frage, ob es einen Rundgang durch Königsberg gibt, der jede der sieben Brücken über den Fluss Pregel genau einmal benutzt.
Aufgabe 3
(a) Versuche erst einmal, das Problem von Euler zu lösen.
(b) Der folgende Graph zeigt die Brückensituation in Königsberg in einer abstrahierenden Darstellung. Was stellen die Knoten des Graphen, was die Kanten dar?
(c) Wie viele Kanten gehen von den jeweiligen Knoten aus? Was hat das mit der Lösung des Problems von Euler zu tun?
Soziale Netzwerke im Internet
Bist du Mitglied eines sozialen Netzwerks im Internet wie Instagram, TikTok, YouTube, Snapchat, Discord, Twitch, X, etc? Dann hast du sicher schon einmal eine Nachricht erhalten, die etwa so aussieht:
An: Daniel Hallo Daniel, Rebekka hat dich als Freund/Freundin auf ... hinzugefügt. Wir benötigen deine Bestätigung, dass du Rebekka kennst, damit ihr Freunde/Freundinnen auf ... sein könnt. Viele Grüße vom ...
Soziale Netzwerke sind Netzgemeinschaften (sogenannte Online-Communities), bei der Menschen über das Internet kommunizieren.
Aufgabe 4
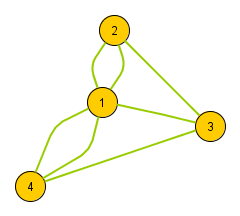
(a) Beschreibe die Struktur des früher sehr beliebten Wer-kennt-wen-Netzwerksmit Hilfe eines Graphen.
Rebekka kennt Daniel, Florian, Lisa, Greta, Sophie, Maria Daniel kennt Tim, Rebekka, Jonas Florian kennt Rebekka, Sophie Lisa kennt Rebekka, Sophie, Jonas Greta kennt Rebekka, Sophie, Tim Sophie kennt Rebekka, Florian, Lisa, Greta Maria kennt Rebekka Tim kennt Daniel, Greta Jonas kennt Daniel, Lisa Martin kennt Markus Markus kennt Martin
(b) Welche Möglichkeiten bieten soziale Netzwerke? Siehst du auch Gefahren bei der Nutzung kommerziell betriebener Online-Communities?
(c) Noch ein soziales Netzwerk:
Anna liebt Ben Ben liebt Clara Clara liebt Daniel Daniel liebt Anna
Wie würde man hier die Vernetzungungsstruktur darstellen?
Ein Umfüllproblem
Zum Nudelkochen im Ferienlager werden genau 2 Liter Wasser benötigt. Zum Abmessen stehen nur ein kleiner Eimer, der 3 Liter fasst, und einen etwas größerer Eimer, der 4 Liter fasst, zur Verfügung. Kann das funktionieren?
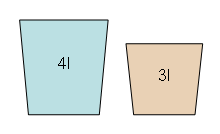
Um systematisch alle durch Umfüllen erzeugbaren Wassermengen zu bestimmen, kann man einen Zustandsgraphen erstellen. Die Knoten des Graphen sind die aktuellen Füllinhalte der beiden Eimer. Die Kanten des Graphen stellen die Umfüllvorgänge dar.
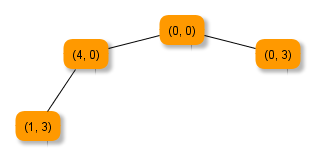
Aufgabe 5
Vervollständige den bereits begonnenen Graphen. Ermittle mit diesem Graphen verschiedene Möglichkeiten, eine 2-Liter-Wassermenge durch Umfüllen zu erzeugen.
Ein Transportproblem
Am Flussufer befinden sich ein Wolf, eine Ziege, ein Kohlkopf und ein Fährmann. Der Fährmann soll Wolf, Ziege und Kohlkopf auf die andere Seite des Flusses bringen. Er kann aber immer nur ein der drei mit an das andere Ufer nehmen und muss die beiden anderen so lange allein lassen. Da nun der Wolfe gerne die Ziege frisst und die Ziege auf den Kohlkopf scharf ist, kann der Fährmann diese Paarungen nicht allein lassen. Kann der Fährmann das Transportproblem lösen?
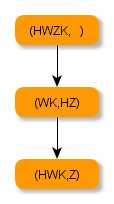
Aufgabe 6
Versuche, das Transportproblem systematisch zu lösen, indem du den bereits begonnenen Transport-Graphen vervollständigst.
Quellen
-
[1]: Zugrundeliegende Ostseekarte - Urheber: Michael Klockmann - Lizenz: Creative Commons BY-SA 3.0
unter Verwendung von:
- Ostseekarte - Urheber: Michael Klockmann - Lizenz: Creative Commons BY-SA 3.0
- [2]: Europakarte - Urheber: CrazyPhunk - Lizenz: Creative Commons BY-SA 3.0
- [3]: Brücken von Königsberg - Urheber: Bogdan Giusca - Lizenz: Creative Commons BY-SA 3.0
- [4]: Fährmann - Urheber: Georg Rab - Lizenz: Public Domain