Der Algorithmus von Moore
Bekanntschaft um mehrere Ecken
Im Alltag kommt es gelegentlich vor, dass jemand sagt: "Den kenne ich um mehrere Ecken". Das heißt dann wohl, dass derjenige jemanden kennt, der wiederum jemanden kennt, der ...
Im Folgenden betrachten wir eine Situation, in der Bekanntschaft durch "ihre / seine Handynummer habe ich gespeichert" festgelegt wird. Dabei sollen folgende Personen mit ihren Bekanntschaften betrachtet werden:
Adriana kennt Clara, Erik, Greta Betül kennt Clara, Dominik Clara kennt Adriana, Dominik, Erik Dominik kennt Betül, Erik Erik kennt Dominik, Greta Fabian kennt Betül, Dominik, Hannah Greta kennt Dominik Hannah kennt Fabian Hannah kennt Greta
Du sollst herausfinden, um "wie viele Ecken" Adriana mit Betül, Clara, Dominik, ..., Hannah bekannt ist.
Aufgabe 1
Ziel ist es, den "Bekanntheitsabstand" von Adriana zu Betül, Clara, Dominik, ..., Hannah zu bestimmen. Dabei soll direkte Bekanntschaft durch den Bekanntheitsabstand 1 beschrieben werden. Versuche (ohne den Bekanntschaftsgraphen zu zeichnen), die gesuchten Bekannheitsabstände systematisch zu ermitteln. Beschreibe dein Vorgehen.
Aufgabe 2
Die Abbildungen zeigen ein Verfahren, wie man systematisch minimale Abstände in einem Graphen ermitteln kann. Beachte, dass "u" hier für "unendlich" steht.
Versuche, anhand der Abbildungen das Verfahren zu erschließen und folgende Fragen zu klären: Welche Knoten werden jeweils grün / blau markiert? Wie kommen die Zahlen (als Zusatzinformationen an den Knoten) zustande? Warum hört das Verfahren nach der letzten Abbildung auf? Wie ist das Ergebnis zu deuten?
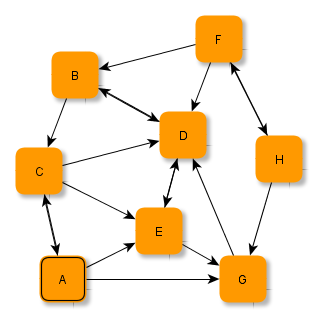
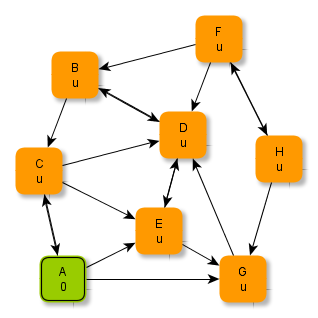
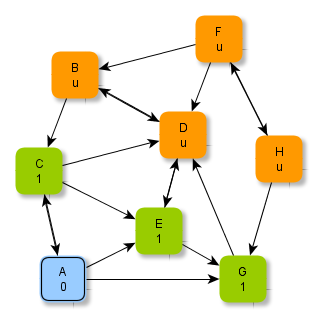
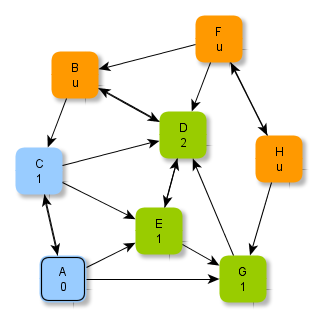
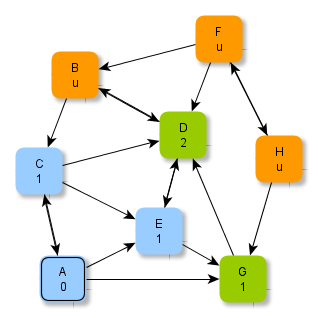
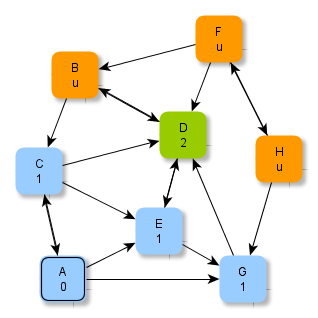
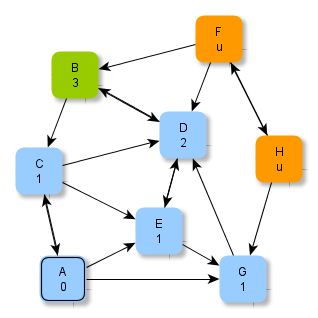
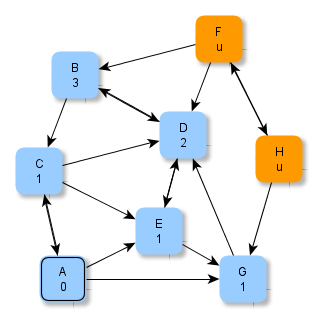
Ein Verfahren zur Bestimmung minimaler Abstände
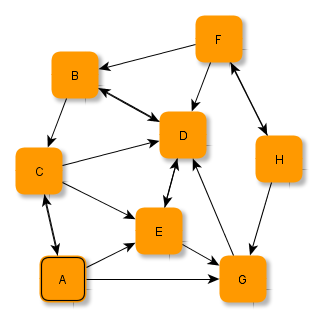
Das Verfahren zur Bestimmung minimaler Abstände soll hier anhand des folgenden Graphen erläutert werden.

Hier ist der Knoten A bereits (durch die Umrandung des Knotens) hervorgehoben. A soll der Startknoten sein, von dem aus die minimalen Abstände zu allen anderen Knoten bestimmt werden sollen.
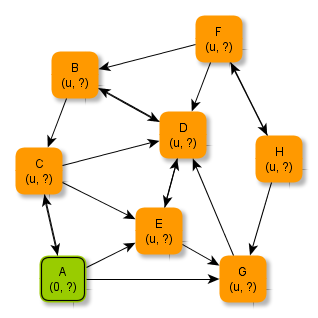
Alle Knoten werden mit einer Zusatzinformation versehen, die den minimalen Abstand zu A beschreiben soll. Zu Beginn beträgt dieser minimale Abstand beim Startknoten 0 und bei allen anderen Knoten u (für unendlich). Diese Information beschreibt das Wissen, das ohne weitere Verarbeitung des Graphen direkt vorliegt.
Der Startknoten A wird hervorgehoben (grün), weil die weitere Verarbeitung bei diesem Knoten beginnt. Die grün markierten Knoten werden mit der Datenstruktur Schlange verwaltet. Beachte, dass sich in dieser Schlange die Knoten mit geringstem Abstand immer ganz vorne befinden.

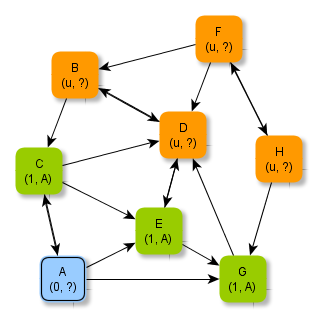
Der Knoten A wird jetzt verarbeitet und "als verarbeitet markiert" (blau): Sämtliche Nachbarn von A werden in die Schlange (mit den noch zu verarbeitenden Knoten (grün)) aufgenommen. Zusätzlich werden die minimalen Abstände dieser Nachbarknoten von A aktualisiert. Man weiß ja, dass diese Abstände 1 betragen.

Aus der Schlange wird der erste Knoten herausgegriffen, verarbeitet und "als verarbeitet markiert" (blau): Sämtliche Nachbarn dieses ausgewählten Knotens, die noch nicht verarbeitet sind, werden in die Schlange aufgenommen. Zusätzlich werden die minimalen Abstände dieser Nachbarknoten des ausgewählten Knotens aktualisiert. Man muss hierzu nur 1 zum Abstand des vorliegenden aktuellen Knotens hinzuzählen.

Aus der Schlange wird der erste Knoten herausgegriffen, verarbeitet und "als verarbeitet markiert" (blau): Sämtliche Nachbarn dieses ausgewählten Knotens, die noch nicht verarbeitet sind, werden in die Schlange aufgenommen. Zusätzlich werden die minimalen Abstände dieser Nachbarknoten des ausgewählten Knotens aktualisiert. Man muss hierzu nur 1 zum Abstand des vorliegenden aktuellen Knotens hinzuzählen.

Aus der Schlange wird der erste Knoten herausgegriffen, verarbeitet und "als verarbeitet markiert" (blau): Sämtliche Nachbarn dieses ausgewählten Knotens, die noch nicht verarbeitet sind, werden in die Schlange aufgenommen. Zusätzlich werden die minimalen Abstände dieser Nachbarknoten des ausgewählten Knotens aktualisiert. Man muss hierzu nur 1 zum Abstand des vorliegenden aktuellen Knotens hinzuzählen.

Aus der Schlange wird der erste Knoten herausgegriffen, verarbeitet und "als verarbeitet markiert" (blau): Sämtliche Nachbarn dieses ausgewählten Knotens, die noch nicht verarbeitet sind, werden in die Schlange aufgenommen. Zusätzlich werden die minimalen Abstände dieser Nachbarknoten des ausgewählten Knotens aktualisiert. Man muss hierzu nur 1 zum Abstand des vorliegenden aktuellen Knotens hinzuzählen.

Aus der Schlange wird der erste Knoten herausgegriffen, verarbeitet und "als verarbeitet markiert" (blau): Sämtliche Nachbarn dieses ausgewählten Knotens, die noch nicht verarbeitet sind, werden in die Schlange aufgenommen. Zusätzlich werden die minimalen Abstände dieser Nachbarknoten des ausgewählten Knotens aktualisiert. Man muss hierzu nur 1 zum Abstand des vorliegenden aktuellen Knotens hinzuzählen.

Jetzt sind alle von A aus erreichbaren Knoten verarbeitet. Die verbleibenden Knoten (gelb) behalten den Abstand "u" (für unendlich).
Der Algorithmus zum Verfahren - Algorithmus von Moore
Das oben beschriebene Verfahren zur Bestimmung minimaler Abstände lässt sich als Algorithmus wie folgt präzisieren:
ALGORITHMUS # von Moore
Übergabedaten: Graph, startKnoten, zielKnoten
# Vorbereitung des Graphen
für alle knoten des Graphen:
setze abstand auf 'u'
setze abstand von startKnoten.abstand auf 0
füge startKnoten in eine Schlange zuVerarbeiten ein
# Verarbeitung der Knoten
SOLANGE die Schlange zuVerarbeiten nicht leer ist:
ausgewaehlterKnoten ist das erste Element aus zuVerarbeiten
entferne ausgewaehlterKnoten aus zuVerarbeiten
für alle nachbarKnoten von ausgewaehlterKnoten:
wenn abstand von nachbarKnoten == 'u':
füge nachbarKnoten hinten in die Schlange zuVerarbeiten ein
neuerAbstand = (abstand von ausgewahlterKnoten) + 1
setze abstand von nachbarKnoten auf neuerAbstand
weglaenge = abstand von zielKnoten
Rückgabedaten: weglaenge
Aufgabe 3
Führe den Algorithmus mit F als Startknoten aus.
Bestimmung kürzester Wege
Zusätzlich zum jeweils bekannten minimalen Abstand wird der Knoten vermerkt, über den der minimale Abstand bestimmt wurde. Die folgenden Abbildungen zeigen die erweiterten Zusatzinformationen.
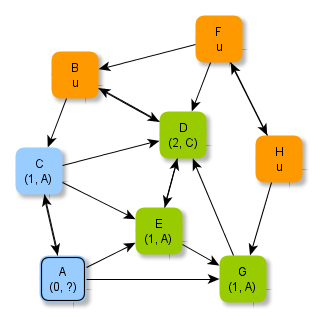
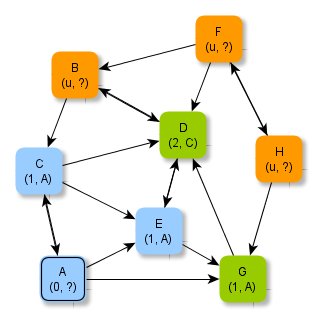
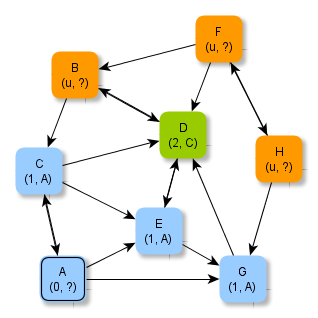
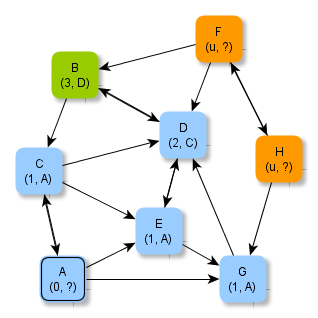
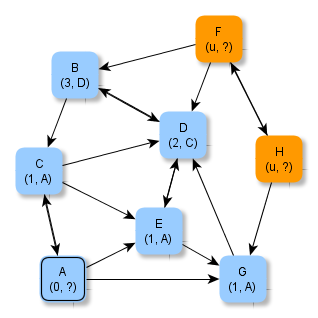
Aufgabe 4
(a) Wie kann man aus den Zusatzinformationen einen kürzesten Weg vom Startknoten zu einem Zielknoten bestimmen?
(b) Es gibt oft mehrere kürzeste Wege zu einem Zielknoten. Welcher dieser Wege wird in dem beschriebenen Verfahren registriert?

