Einen Knoten in einen Binärbaum einfügen

Neues Klassendiagramm

Ein Algorithmus zum Einfügen ist natürlich auch unabhängig von unserem Beispiel schon sinnvoll, damit unsere Binärbaumklasse eine Einfügeprozedur hat, wir also neue Knoten nicht immer manuell einfügen müssen. Denn wie Du gewiss bemerkt hast, macht es keinen Spaß, einen Binärbaum von Hand zu erstellen und dabei jeden Knoten von Hand korrekt zu positionieren. Wir wollen also unser Klassendiagramm folgendermaßen erweitern:

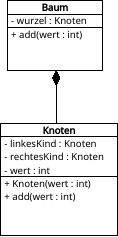
Die Idee

Wenn wir ein neues Element in einen bereits bestehenden Binärbaum einfügen wollen, müssen wir es eigentlich nur irgendwo im Speicher ablegen und einem bereits bestehenden Knoten einen Zeiger auf diese Speicherzellen geben.

Dabei müssen wir natürlich darauf achten, dass unsere Binärbaumeigenschaften nicht verletzt werden, also dass nach dem Einfügen nach wie vor gilt, dass

• Jeder Knoten (außer der Wurzel) hat mindestens einen Vater und höchstens zwei Kinder
• Der rechte Unterbaum eines Knotens ist größer als der Knoten, der Linke kleiner.

Wir können uns beim Einfügen eigentlich wunderbar an unserem Suchalgorithmus orientieren:

Zunächst prüfen wir, ob der neue Schlüssel größer (oder gleich), oder kleiner als die Wurzel ist. Ist er größer, prüfen wir, ob die Wurzel ein rechtes Kind hat. Wenn nicht, geben wir einfach der Wurzel den entsprechenden Zeiger. Analog gehen wir vor, wenn der Schlüssel kleiner ist.

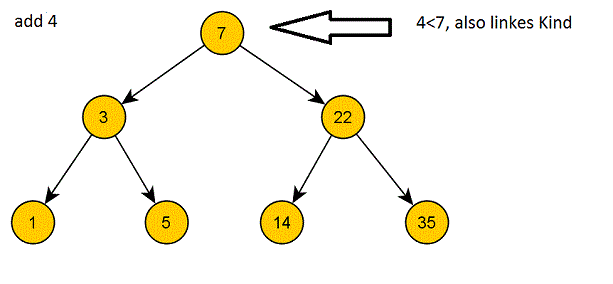
Hat die Wurzel einen derartigen Zeiger bereits, gehen wir zu dem Element, auf das dieser Zeiger zeigt und gehen hier genau analog vor, fügen also entweder das Element als Kind dieses Elements ein, oder prüfen es wieder eine Stufe tiefer.

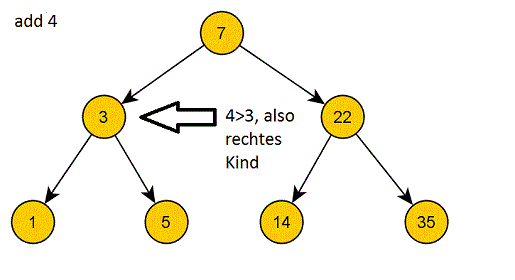
So können wir immer weiter vorgehen, bis wir einen Knoten gefunden haben, der kein entsprechendes Kind hat (was spätestens der Fall ist, wenn wir ein Blatt erreichen).

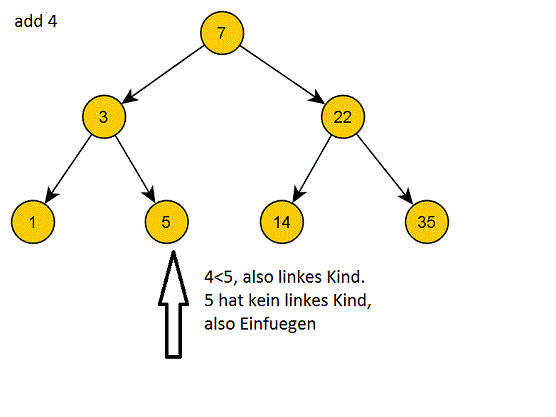
Aufgabe 1

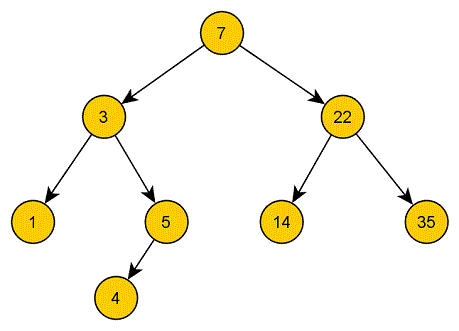
(a) Führe die add-Prozedur an finalen obigen Baum mit den Schlüsseln 2, 33 und 44 von Hand aus.

(b) Wie viele Vergleiche werden im worst-case für eine Einfüge-Prozedur benötigt?

(c) Wie viele Vergleiche werden im best-case für eine Einfüge-Prozedur bei einem höhenbalancierten Binärbaum benötigt?

Der Algorithmus

Wenn Du nicht bereits selbst einen Algorithmus entworfen und implementiert hast, solltest Du versuchen, den gerade vorgestellten Algorithmus selbst zu implementieren. Damit Du den Algorithmus aber auf jeden Fall einmal gesehen hast, siehst Du im folgenden eine mögliche Implementation:

class Knoten(object):
    def __init__(self, wert):
        self.wert = wert
        self.linkesKind = None
        self.rechtesKind = None

    def add(self, wert):
        if wert < self.wert:
            if self.linkesKind == None:
                self.linkesKind = Knoten(wert)
            else:
                self.linkesKind.add(wert)
        else:
            if self.rechtesKind == None:
                self.rechtesKind = Knoten(wert)
            else:
                self.rechtesKind.add(wert)

class Baum(object):
    def __init__(self):
        self.wurzel = None

    def add(self, wert):
        if self.wurzel == None:
            self.wurzel = Knoten(wert)
        else:
            self.wurzel.add(wert)
</neuerknoten.wert>