Einen Knoten aus einem Binärbaum löschen
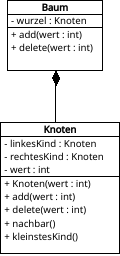
Neues Klassendiagramm
Analog zum Einfügealgorithmus, ist natürlich auch unser Löschalgorithmus etwas, was unserem Binärbaum im Allgemeinen gut zu Gesicht steht:
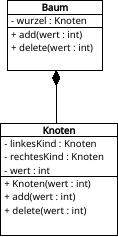
Wie auch bei der Einfügeprozedur, kannst Du dir zunächst selbst versuchen, einen Algorithmus zu überlegen. Dieser ist zwar etwas komplizierter, als add, aber wenn Du zumindest siehst, wo das Problem liegt, verstehst Du den unten vorgestellten delete besser. Und vielleicht gelingt es dir ja trotzdem.
Problem
Um ein Element aus einem Binärbaum zu löschen, müssen wir es zunächst finden. Wenn wir den Schlüssel nun gefunden haben, können wir ihn natürlich löschen, aber was passiert dann? Dann haben wir entweder die Wurzel gelöscht, und somit keinen Baum mehr:
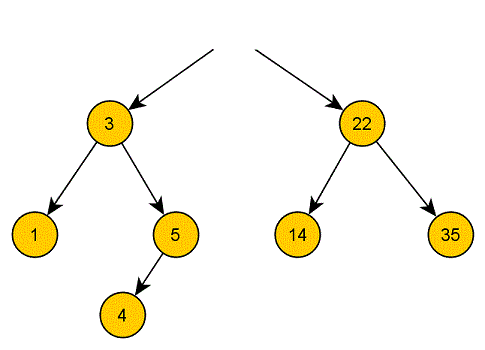
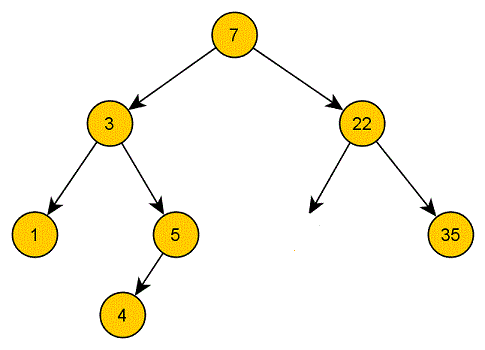
Löschen wir einen inneren Knoten, haben wir plötzlich Knoten, die keinen Vaterknoten mehr haben und somit praktisch nicht mehr Teil unseres Baums sind. Schließlich gibt es keine Möglichkeit, sie mithilfe der existierenden Zeiger von der Wurzel zu erreichen:
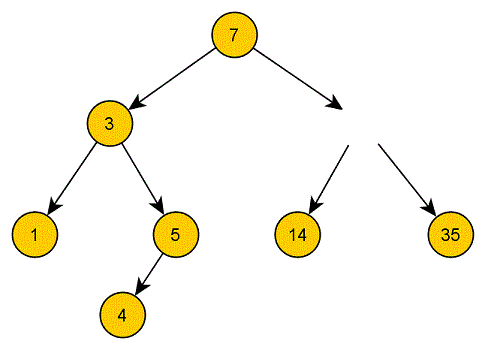
Löschen wir ein Blatt, haben wir kaum ein Problem. Das einzige, was hier stört ist, dass wir einen überflüssigen Zeiger rumfliegen haben:
Idee der Lösung
Um unsere Löschung jetzt korrekt durchzuführen, müssen wir die Fälle einzeln abhandeln:
Bei der Löschung unseres Blatts, können wir natürlich einfach auch den Zeiger löschen:
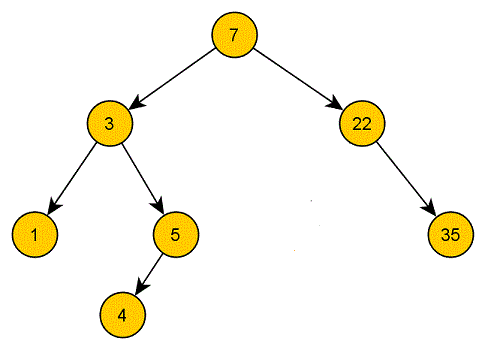
Wollen wir einen inneren Knoten löschen, können wir zwischen zwei Sonderfällen unterscheiden, nämlich einmal dem simplen, in dem unser Knoten nur ein Kind hat:
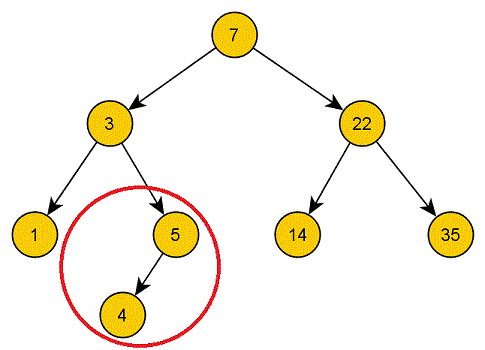
In dem Fall können wir einfach das eine Kind des zu löschenden Knoten an die Stelle des zu löschenden Knoten setzen. Die Position der Kinder und Kindeskinder des entsprechenden Knotens ist natürlich weiterhin korrekt und so wie wir unsere Binärbäume aufbauen passt auch die Position des verschobenen Knotens.
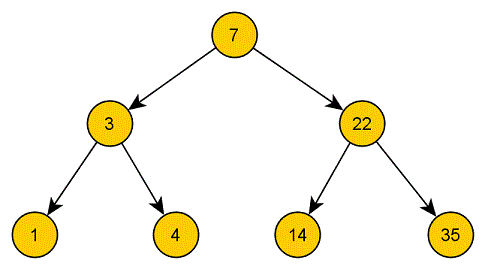
Das selbe funktioniert auch, wenn die Wurzel nur ein Kind hat:
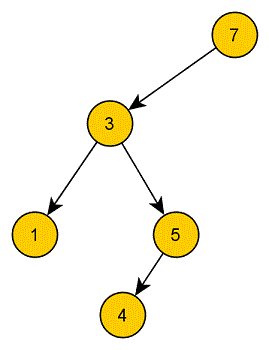
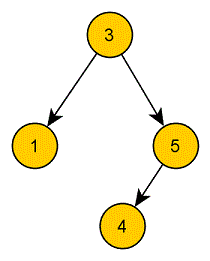
Hat ein Knoten zwei Kinder, können wir ihn am besten durch einen direkten Nachbarn innerhalb des Unterbaums des zu löschenden Knotens ersetzen. Mit direktem Nachbarn ist der Knoten innerhalb der genannten Knotengruppe gemeint, der entweder der nächstgrößte oder nächstkleinste (das ist egal) gemeint. Man nennt diesen Nachbarn in-order Nachbar.
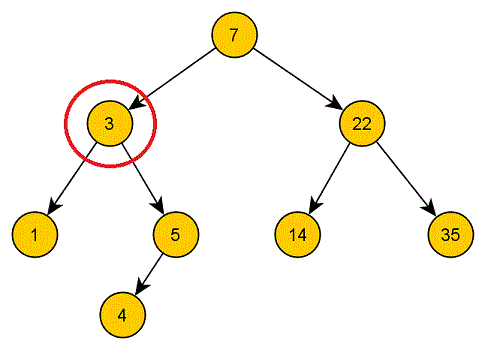
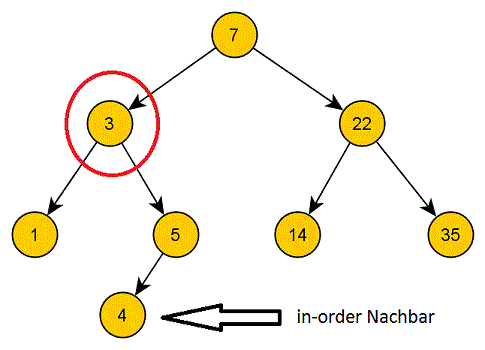
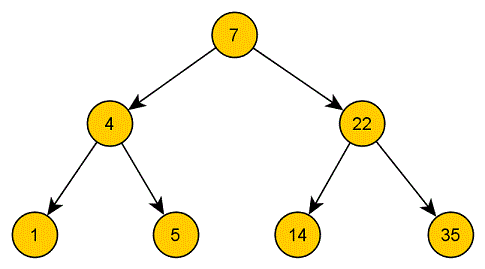
Hat der in-order Nachbar unseres zu löschenden Knoten selbst Kinder, kann er höchstens ein Kind haben (sonst wäre eines der Kinder der in-order Nachbar).
Wenn wir diesen also verschieben, löschen wir unten im Prizip wieder entweder ein Blatt oder einen Knoten mit nur einem Kind und können uns auf unsere Ideen von zuvor zurückziehen.
Aufgabe 13
(a) Nutze die Idee des Algorithmus, um von Hand die Knoten 3, 7 und 35(in dieser Reihenfolge) zu löschen.
(b) Wie viele Vergleiche werden benötigt, um ein Blatt zu löschen? Wie viele andere Schritte?
(c) Wie viele Vergleiche werden benötigt, um einen inneren Knoten zu löschen? Wie viele andere Schritte?
Der Algorithmus
Wenn Du nicht bereits selbst einen Algorithmus entworfen und implementiert hast, solltest Du versuchen, den gerade vorgestellten Algorithmus selbst zu implementieren. Damit Du den Algorithmus aber auf jeden Fall einmal gesehen hast, siehst Du im folgenden eine mögliche Implementation:
class Knoten(object):
def __init__(self, wert):
self.wert = wert
self.linkesKind = None
self.rechtesKind = None
def add(self, wert):
if wert < self.wert:
if self.linkesKind == None:
self.linkesKind = Knoten(wert)
else:
self.linkesKind.add(wert)
else:
if self.rechtesKind == None:
self.rechtesKind = Knoten(wert)
else:
self.rechtesKind.add(wert)
def delete(self, key):
print("delete", key, self.wert)
if key < self.wert:
if self.linkesKind != None:
neuesLinkes = self.linkesKind.delete(key)
self.linkesKind = neuesLinkes
return self
else:
if self.linkesKind != None:
return None
else:
return self
elif key > self.wert:
if self.rechtesKind != None:
neuesRechtes = self.rechtesKind.delete(key)
self.rechtesKind = neuesRechtes
return self
else:
if self.rechtesKind != None:
return None
else:
return self
else:
if self.linkesKind == None:
return self.rechtesKind
elif self.rechtesKind == None:
return self.linkesKind
else:
nachbar = self.nachbar()
self.wert = nachbar.wert
self.rechtesKind = self.rechtesKind.delete(self.wert)
return self
def nachbar(self):
if self.rechtesKind.linkesKind == None:
return self.rechtesKind
else:
return self.rechtesKind.kleinstesKind()
def kleinstesKind(self):
if self.linkesKind.linkesKind == None:
return self.linkesKind
else:
return self.linkesKind.kleinstesKind()
class Baum(object):
def __init__(self):
self.wurzel = None
def add(self, wert):
if self.wurzel == None:
self.wurzel = Knoten(wert)
else:
self.wurzel.add(wert)
def delete(self, key):
if self.wurzel == None:
return
self.wurzel = self.wurzel.delete(key)
</neuerknoten.wert>
Da wir zum Implementieren der delete Prozedur einige Hilfsprozeduren einführen mussten, sollten wir diese nun auch in unser Klassendiagramm aufnehmen: