Problemreduktion
Das Problem auf ein analoges zurückführen
Wir betrachten weiterhin ein gitterförmiges Wegenetz und entwickeln Eigenschaften der Funktion anzahlWege.
Aufgabe 1
-
Begründe anhand der Abbildung: Ein (kürzester) Weg zum Punkt (9,4) führt entweder über den Punkt (8,3)
oder über den Punkt (8,4).
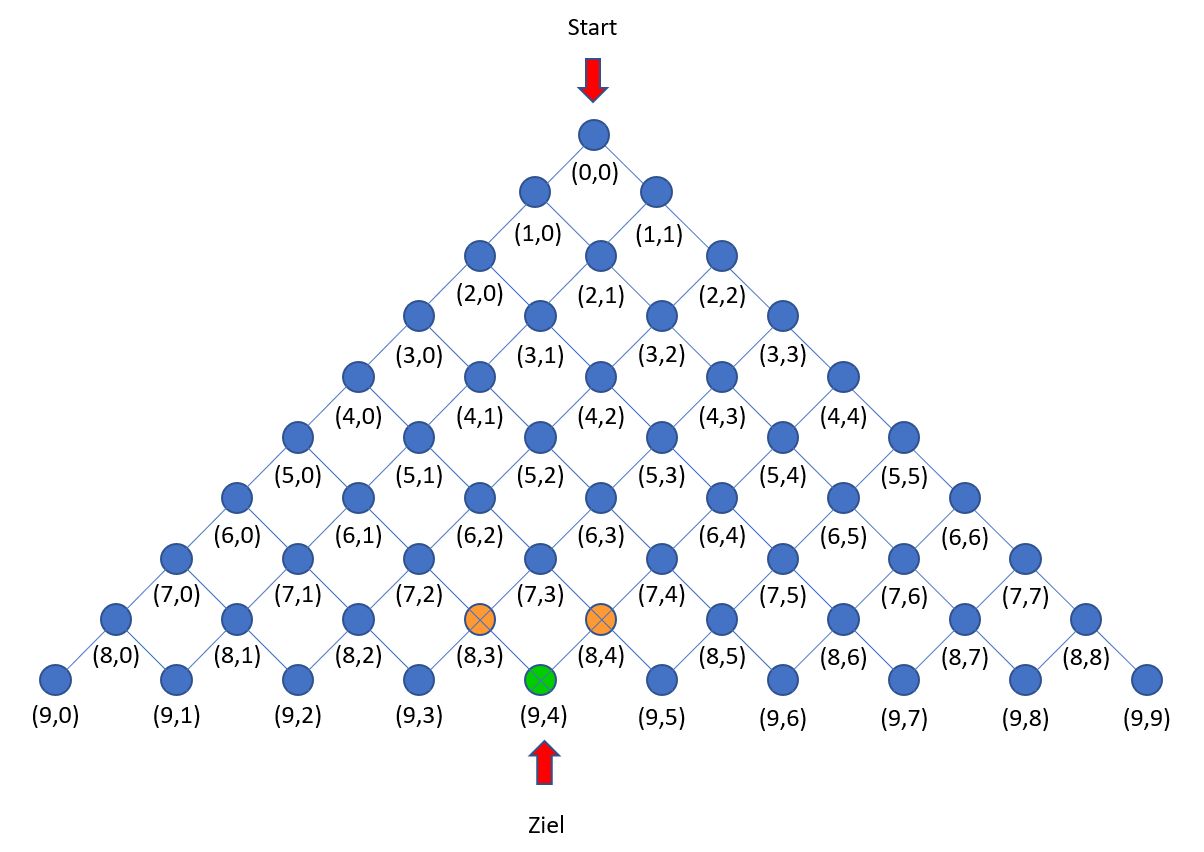
-
Begründe: Man erhält daher den folgenden Problemreduktionsschritt:
anzahlWege 9 4 -> anzahlwege 8 3 + anzahlWege 8 4
Aufgabe 2
Die in Aufgabe 1 durchgeführte Argumentation kann man auf alle inneren Punkte des Punktgitters übertragen.
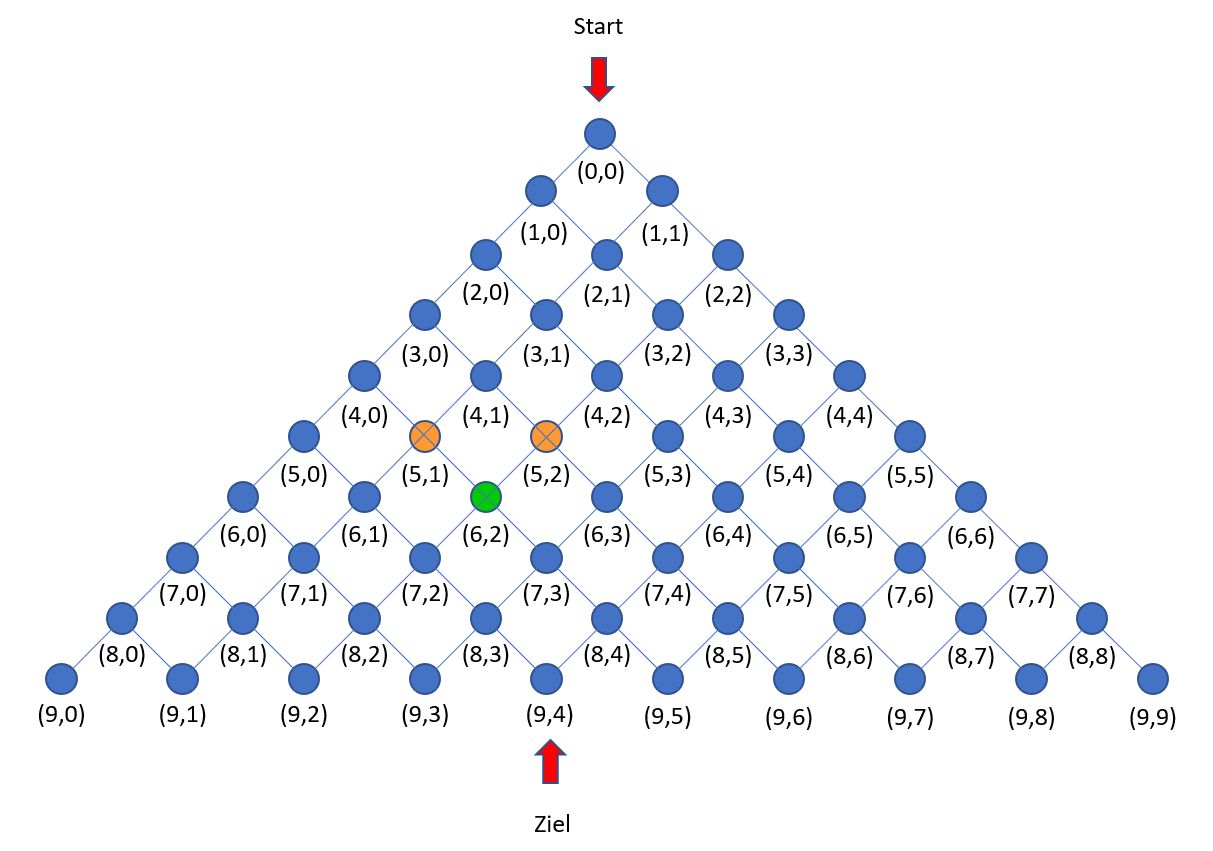
- Ergänze den Problemreduktionsschritt:
anzahlWege 6 2 -> anzahlwege ... ... + anzahlWege ... ... -
Verallgemeinere den Problemreduktionsschritt für innere Punkte:
Falls k > 0 und k < n: anzahlWege n k -> anzahlwege ... ... + anzahlWege ... ...
Aufgabe 3
Begründe: Für einen Punkt am linken Rand des Punktgitters kann man die Anzahl der kürzesten Wege direkt angeben.
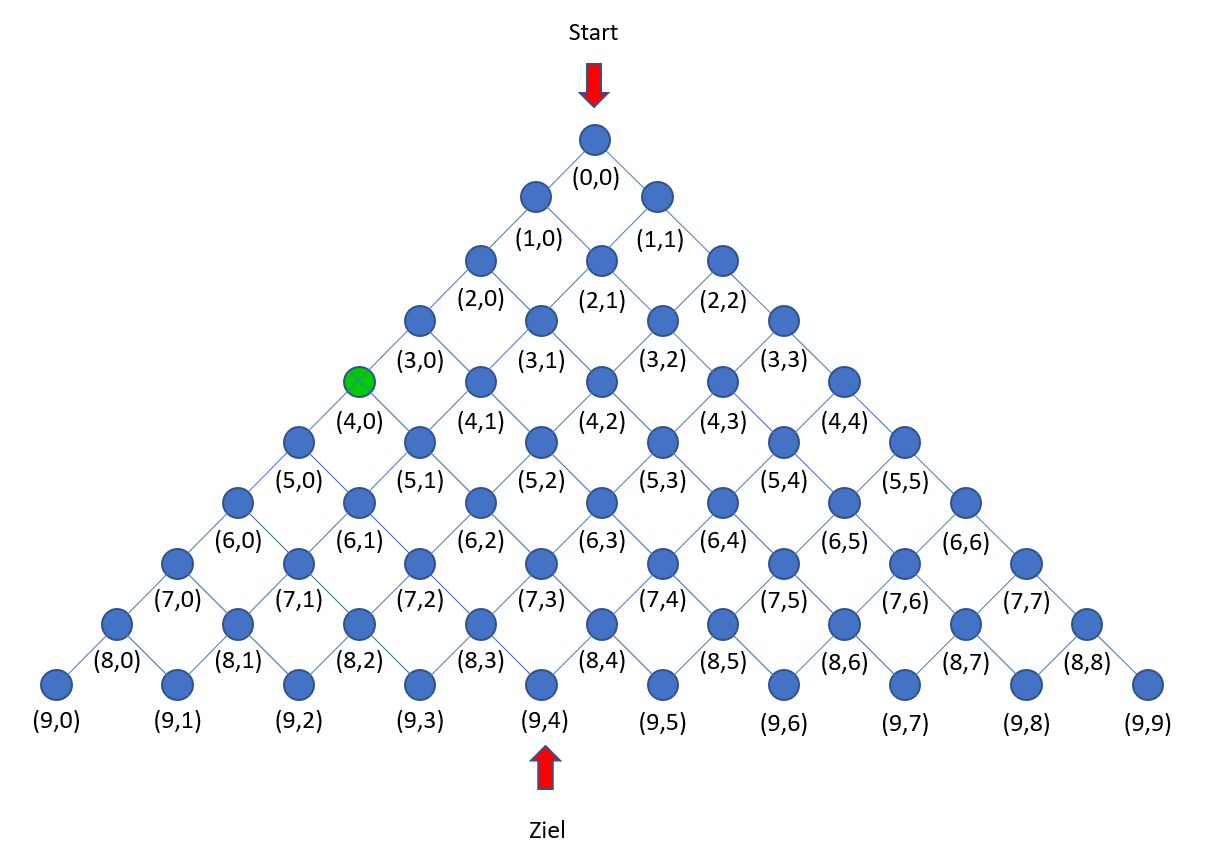
-
Begründe den Reduktionsanfang:
anzahlWege 4 0 -> 1 -
Begründe den verallgemeinerten Reduktionsanfang:
Falls k == 0: anzahlWege n k -> 1
Aufgabe 4
Begründe: Für einen Punkt am rechten Rand des Punktgitters kann man die Anzahl der kürzesten Wege ebenfalls direkt angeben.
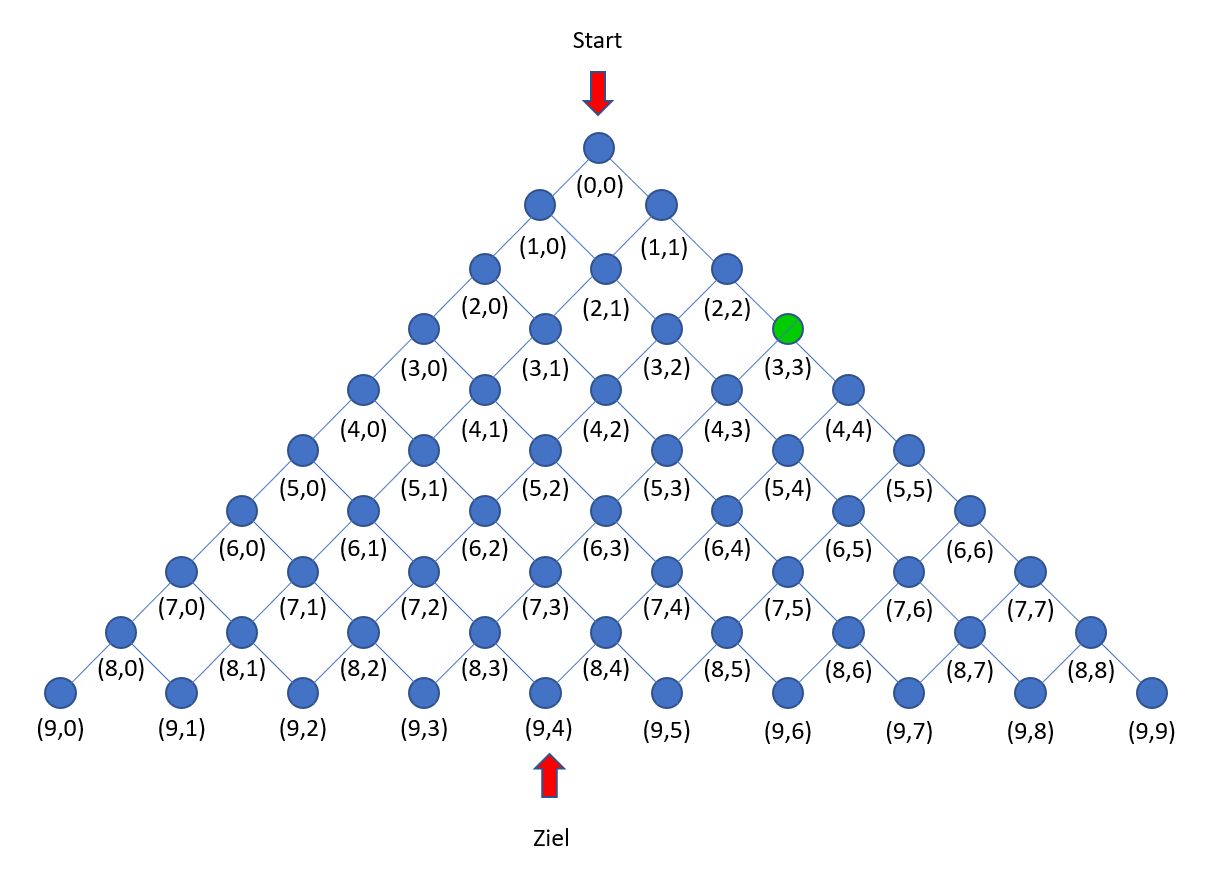
- Ergänze den Reduktionsanfang:
anzahlWege 3 3 -> ... - Ergänze den verallgemeinerten Reduktionsanfang:
Falls ...: anzahlWege n k -> ...
Aufgabe 5
In den Reduktionsschritten haben wir ein Verfahren benutzt, das man rekursive Problemreduktion nennt. Es besagt: Reduziere das Problem auf ein entsprechendes, aber verkleinertes Problem. Erläutere das Verfahren im aktuellen Kontext. Was bedeutet hier "entsprechend" und was bedeutet "verkleinert"?

