Reduktion von Ausdrücken

Wie werden Ausdrücke in Racket ausgewertet?

Das Konzept eines Ausdrucks begleitet uns bereits seit dem ersten Kapitel dieser Lerneinheit. Worüber wir uns allerdings noch keine genaueren Gedanken gemacht haben, ist wie die teils sehr komplexen und ineinander verschachtelten Ausdrücke zu einem Wert ausgewertet werden. Diesen schrittweisen Prozess wollen wir uns in diesem Kapitel anschauen. DrRacket bietet hierzu ein hilfreiches Tool an: den Stepper. Um diesen jedoch bestmöglich nutzen zu können, arbeiten wir in diesem Kapitel zum ersten Mal mit einer anderen Racket-Version.

Anmerkung: Auch die bisher genutzte Racket-Version Schreibe Dein Programm! besitzt theoretisch einen Stepper. Zum Zeitpunkt der Erstellung dieses Kapitels ist dieser jedoch nicht voll funktionsfähig, weswegen auf eine alternative Racket-Version ausgewichen wird.

Aufgabe 1: Vorbereitung von DrRacket

(a) Ändere deine verwendete Racket-Version in DrRacket. Klicke hierzu in DrRacket unten links auf deine aktuelle Version und wähle anstelle von Schreibe Dein Programm! die Version Intermediate Student with lambda aus.

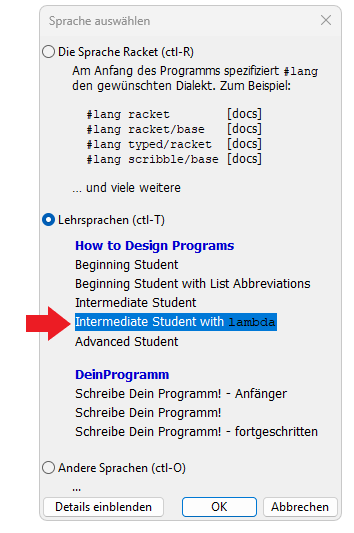
Die Racket-Version Intermediate Student with lambda

Die hier genutzte Racket-Version stammt aus dem US-amerikanischen Lehrbuch How to Design Programs und weist in ihrer Funktionalität und Syntax eine sehr hohe Ähnlichkeit zur bisher genutzten Version Schreibe Dein Programm! auf. Zwei Unterschiede seien an dieser Stelle jedoch vermerkt:

1. Datentypen werden in dieser Version immer groß geschrieben. Eine korrekte Signaturdefinition wäre daher exemplarisch: (: function (String Natural -> Boolean))
2. Die REPL-Ausgaben der Versionen unterscheiden sich an mehreren Stellen. So werden beispielsweise boolesche Werte anstelle von #t und #f als #true und #false ausgegeben.

Aufgabe 2: Reduktion von verketteten Ausdrücken

(a) Berechne ohne die Hilfe von Racket die folgenden beiden Rechnungen. Achte dabei einmal darauf, in welchen Schritten du diese im Kopf löst.

• $2 \cdot (3+1)$
• $(10 - (4 + 1)) \cdot (2 + 2)$

Genau wie wir in unserem Kopf schrittweise vorgehen, um notwendige Teillösungen zu berechnen, arbeitet auch Racket einen Ausdruck ab: Schritt für Schritt.

(b) Schreibe in das Definitionsfenster einen Ausdruck der $2 \cdot (3+1)$ berechnet.

Mit dem Stepper von DrRacket können wir uns nun anzeigen lassen, wie Racket die im Definitionsfenster geschriebenen Ausdrücke auswertet.

(c) Drücke oben rechts in DrRacket auf Stepper. Der Stepper besteht aus einer linken und einer durch einen roten Pfeil abgetrennten rechten Hälfte. Beide Hälften zeigen jeweils einen Ausdruck an. Der linke Ausdruck stellt den Ausdruck dar, der aktuell von Racket ausgewertet wird. Innerhalb des linken Ausdrucks ist der Teilausdruck grün markiert, der im nächsten Schritt ausgewertet wird. Der rechte Ausdruck stellt den durch den nächsten Auswertungsschritt entstehenden Ausdruck dar, in welchem der ausgewertete Teilausdruck lila markiert ist.

Im unteren Beispielbild wird der Ausdruck (* 2 (+ 3 1)) ausgewertet, im ersten Schritt wird der innere grün markierte Teilausdruck (+ 3 1) zum lila markierten Wert 4 ausgewertet. Bei klicken auf Next wird der nächste Auswertungsschritt angezeigt. Somit wird der aktuelle rechte Ausdruck nun zum neuen auszuwertenden Ausdruck links.

(d) Führe den Stepper für dein in (b) entworfenen Ausdruck vollständig aus.

(e) Führe den Stepper mit einem Ausdruck aus der $(10 - (4 + 1)) \cdot 4$ berechnet.
Hinweis: Der Stepper führt bei Ausführung alle Ausdrücke aus, die im Definitionsfenster stehen. Es kann also hilfreich sein Ausdrücke, die dich aktuell nicht interessieren, auszukommentieren oder zu löschen.

(f) Beschreibe die in der Auswertung stattfindenden Schritte.

Auswertungsreihenfolge in Racket

Anhand von Aufgabe 2 wurde die allgemeine Auswertungsreihenfolge in Racket bereits sichtbar: von der innersten Klammer zur äußersten und von links nach rechts. Offengeblieben ist jedoch, wie die Übergabedaten in den Funktionskörper eingesetzt werden und wie die Ersetzung von Definitionen abläuft. Dies wollen wir uns im Folgenden noch genauer ansehen.

Aufgabe 3: Reduktion von anonymen Funktionsanwendungen

(a) Analysiere den folgenden Ausdruck und stelle sicher, dass du verstehst, welche Funktionalität dieser erfüllt. Führe anschließend den Stepper für den Ausdruck aus.

( (lambda (x) (+ x 1)) 9)

(b) Analysiere den folgenden Ausdruck und stelle sicher, dass du verstehst, welche Funktionalität dieser erfüllt. Führe anschließend den Stepper für den Ausdruck aus.

( (lambda (s) (string-append "Hallo" s)) "Name")

(c) Beschreibe die in der Auswertung stattfindenden Schritte.

Aufgabe 4: Reduktion von definierten Funktionsanwendungen

(a) Analysiere die folgenden Ausdrücke und stelle sicher, dass du verstehst, welche Funktionalitäten diese erfüllen. Führe anschließend den Stepper für die Ausdrücke aus.

(define inc
  (lambda (x)
    (+ x 1)))

(inc 9)

(b) Analysiere die folgenden Ausdrücke und stelle sicher, dass du verstehst, welche Funktionalitäten diese erfüllen. Führe anschließend den Stepper für die Ausdrücke aus.

(define point-curry
  (lambda (x)
    (lambda (y)
      (lambda (z)
        (list x y z)))))


(((point-curry 2) 4) 8)

(c) Beschreibe die in der Auswertung stattfindenden Schritte.