Übungen: Definitionen
Aufgabe 1: Definition geometrischer Formen
(a) Die von uns genutzte Racket-Version bietet die Möglichkeit, geometrische Formen darzustellen.
Teste hierzu die folgenden REPL-Eingaben:
Sollte die Fehlermeldung "Variable ist nicht definiert" erscheinen, starte deine Racket-Datei nochmals
über den grünen Startknopf oben rechts.
> (square 40 "outline" "red")
> (circle 20 "solid" "green")
> (triangle 60 "solid" "purple")
(b) Die geometrischen Formen lassen sich auch kombiniert darstellen. Teste hierzu die folgenden REPL-Eingaben:
> (above (square 40 "outline" "red") (circle 20 "solid" "green"))
> (beside (square 40 "outline" "red") (triangle 60 "solid" "purple"))
(c) Schreibe in dein Definitionsfenster ein Programm, das bei Ausführung alle der unten gelisteten Darstellungen produziert. Überlege dir hierfür genau, welche Programmelemente du als Definition festlegen möchtest, um ein möglichst kurzes Programm zu schreiben.
Erste Darstellung:
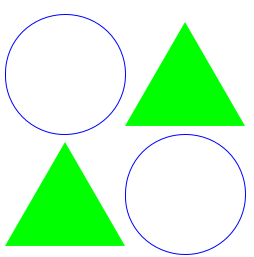Zweite Darstellung:
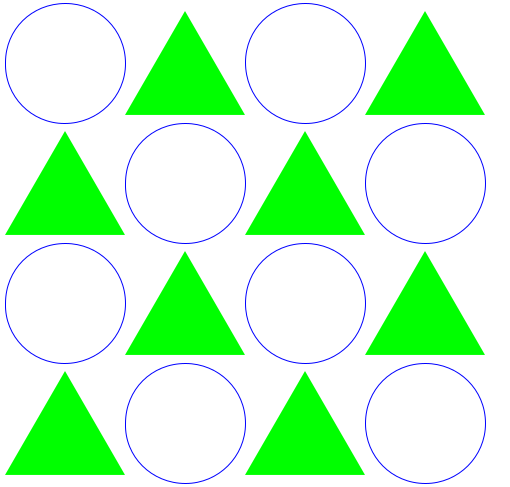Dritte Darstellung:
Vierte Darstellung:
Diese Aufgabe wurde maßgeblich vom Lehrbuch "Schreibe Dein Programm!"
[1]
inspiriert.
Aufgabe 2: Mitternachtsformel
(a) Wir möchten eine Funktion schreiben, die uns eine quadratische Gleichung löst. Hierfür wollen
wir die Mitternachtsformel (abc‑Formel) nutzen. Vervollständige die Funktion Mitternachtsformel:
;Löst eine quadratische Gleichung der Form a*x^2 + b*x + c = 0
(: mitternachtsformel (real real real -> (list-of real)))
;x^2 - 3x - 4 = 0
(check-expect (mitternachtsformel 1 -3 -4) (list 4 -1))
; x^2 - 2x + 1 = 0
(check-expect (mitternachtsformel 1 -2 1) (list 1))
; x^2 + 1 = 0
(check-expect (mitternachtsformel 1 0 1) empty)
(define mitternachtsformel
(lambda (a b c)
...
) )
Die Mitternachtsformel (abc‑Formel) ist eine Methode, um die Lösungen einer quadratischen Gleichung zu finden.
Sie wird verwendet, wenn du eine Gleichung der Form $ax^2 + bx + c = 0$ nach $x$ lösen möchtest.
Die Formel lautet:
$x_{1/2} = \frac{-b \pm \sqrt{b^2-4ac}}{2a}$
Den Ausdruck unter der Wurzel ($b^2-4ac$) nennen wir die Diskriminante (d).
Die Diskriminante gibt Auskunft darüber, wie viele Lösungen die Gleichung hat.
- Wenn $d > 0$ gibt es zwei Lösungen
- Wenn $d = 0$ gibt es eine Lösung
- Wenn $d < 0$ gibt es keine (reelle) Lösung
Quellen
- [1]: Lehrbuch - Schreibe Dein Programm!(letzter Zugriff: 21.07.2025) - Urheber: Michael Sperber, Herbert Klaeren - Lizenz: Creative Commons BY-SA 4.0 International
