Übungen
Aufgabe 1: chuck-a-luck - Ein vorgegebenes Datenmodell interpretieren und implementieren
Beim chuck-a-luck-Spiel soll ein Objekt der Klasse Spiel alle beteiligten Objekte verwalten
und die Spielaktionen als Operationen zur Verfügung stellen.
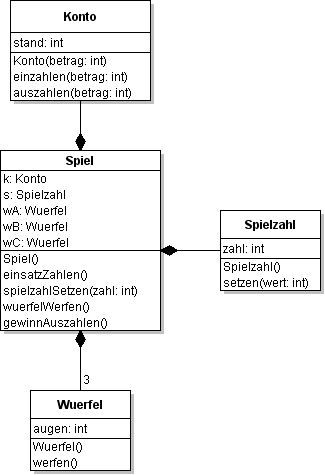
(a) Skizziere ein Objektdiagramm zur Miniwelt chuck-a-luck
.
(b) Woran erkennt man im vorgegebenen Klassendiagramm, dass das Spiel-Objekt für die Erzeugung
der weiteren Objekte zuständig ist? Welche weiteren Zuständigkeiten hat das Spiel-Objekt?
(c) Implementiere dieses Modell. Teste es mit dem folgenden Testprogramm.
from chuckaluck import *
# Erzeugung der Objekte
spiel = Spiel()
# Durchführung eines Spiels
spiel.einsatzZahlen()
spiel.spielzahlSetzen(5)
spiel.wuerfelWerfen()
spiel.gewinnAuszahlen()
# Ausgabe der Spiel
print("Würfel A:", spiel.wuerfelA.augen)
...
Aufgabe 2: Populationsentwicklung - Ein vorgegebenes Datenmodell implementieren
Das folgende Klassendiagramm zeigt ein System, mit dem man die Entwicklung einer Population simulieren kann.
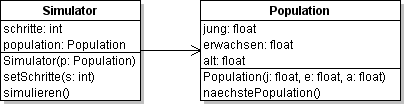
(a) Implementiere die Klasse Population so, dass die Mäusepopulation aus
Modellierung einer Mäusepopulation
als Miniwelt erfasst wird.
(b) Implementiere die Klasse Simulator so, dass sie die Entwicklung der verwalteten Population
beschreibt.
(c) Erstelle ein geeignetes Testprogramm, um die Implementierung zu überprüfen.
(d) Was müsste am Datenmodell verändert werden, wenn man die Population aus dem Miniprojekt modellieren wollte?
Aufgabe 3: Ein Datenmodell erstellen
Ein Zahlenschloss bestehe aus drei Einstellrädern, mit denen die Ziffern der Schlüsselzahl einzeln eingestellt werden können. Hat man die Schlüsselzahl richtig getroffen, dann ist das Schloss offen.
Entwickle ein objektorientiertes Datenmodell, das die vorliegende Miniwelt möglichst strukturgetreu beschreibt. Stelle das Datenmodell auch mit Hilfe von UML-Diagrammen dar.
Implementiere und teste das Datenmodell.
Aufgabe 4: Ein Datenmodell erstellen
Eine Pixelgrafik im pbm-Format hat folgenden Aufbau (vergl. Einstieg - Pixelgrafik):
P1 24 36 000000000000000000000000 000000000000000000000000 000000000000000000000000 000000000000000000000000 000000000000000000000000 000000000000000000000000 000000000000010000000000 000000000000110000000000 000000000000100000000000 000000000011110000000000 000000000110110000000000 000000001111111100000000 000000010001110010000000 000001110001110011000000 000001100111110011100000 000001100000001001100000 000000000000001011100000 000000000000000000110000 000000000000000011110000 000000000000000110011000 000000000000000010111000 000000000000000111111000 000000000000000001011100 000000000000000011011100 000000000000000111111100 000000000000000011101110 000000000000000011111011 000000000000000011011111 000000000000000011101111 000000000000000001101011 000000000000000001010111 000000000000000001111110 000000000000000001111000 000000000000000000110111 000000000000000000111111 000000000000000000011000
Beachte, dass die Zeilenumbrüche zur Darstellung der Nullen und Einsen optional sind. Man könnte also auch alle Nullen und Einsen in eine einzige Zeile schreiben.
P1 24 36 000000000000000000000000...000000000000000000011000
Entwickle ein objektorientiertes Datenmodell, das die Miniwelt Bild im pbm-Format
möglichst
strukturgetreu beschreibt.
Überlege dir hierzu auch Operationen (wie z.B. das Invertieren), die ein Pixelgrafik-Objekt zur Verfügung stellen könnte.
Implementiere und teste das Datenmodell.
Quellen
- [1]: Zahlenschloss - Urheber: Oldie~commonswiki - Lizenz: CC BY-SA 3.0