Gewinnstrategie
Nim-Spiel - einfache Variante
Die Abbildung zeigt mögliche Spielabläufe, wenn ein Spieler S mit einem Zug die Spielposition 5 erreicht.
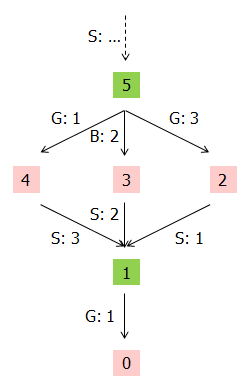
Aufgabe 1
(a) Argumentiere, dass der Gegenspieler G nicht mehr gewinnen kann, wenn Spieler S richtig weiterspielt. Die Spielposition 5 ist somit eine Gewinnposition für einen Spieler.
(b) Argumentiere analog, dass die Spielpositionen 9, 13, ... Gewinnpositionen beim Ein-Haufen-Nim-Spiel sind.
Nim-Spiel - schwierigere Variante
Bei mehreren Haufen ist es nicht mehr ganz so leicht, alle Gewinnpositionen anzugeben.
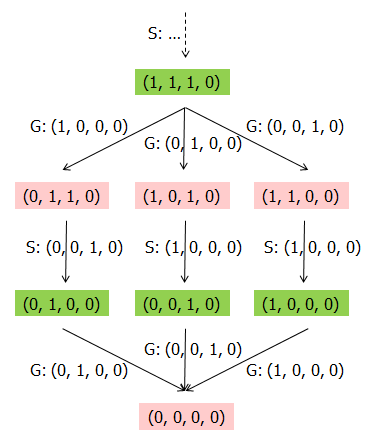
Aufgabe 2
(a) Es ist klar, dass die Positionen (1, 0, 0, 0), (0, 1, 0, 0), (0, 0, 1, 0) und (0, 0, 0, 1) Gewinnpositionen für einen Spieler sind. Warum?
(b) Die Abbildung zeigt, dass die Position (1, 1, 1, 0) ebenfalls eine Gewinnposition für einen Spieler darstellt. Erläutere die Argumentation.
(c) Hier weitere Gewinnpositionen für einen Spieler:
(0, 2, 2, 0), (0, 2, 0, 2), (0, 3, 3, 0), ... (1, 1, 2, 2), (1, 1, 3, 3), (1, 3, 1, 3), ... (1, 2, 3, 0), (1, 0, 3, 2), (0, 3, 2, 1), ...
Zeige dies für ausgewählte Positionen.
(d) Finde selbst weitere Gewinnpositionen.

