Ein Primzahltestalgorithmus
Das Primzahltestproblem
Beim Primzahltestproblem geht es darum, bei einer vorgegebenen natürlichen Zahl zu überprüfen, ob sie eine Primzahl ist oder nicht.
Beispiel: Ist die Zahl 551 eine Primzahl?
Aufgabe 1
Prüfe, ob 551 eine Primzahl ist. Du kannst Python als eine Art Taschenrechner benutzen. Mit dem modulo-Operator %
kannst du den Rest bei einer ganzzahligen Division bestimmen.
Ein einfacher Primzahltestalgorithmus
Wie kann man überprüfen, ob eine natürliche Zahl n (größer als 1) eine Primzahl ist? Ein ganz einfaches Verfahren würde wie folgt funktionieren:
Teile n der Reihe nach von 2 bis n-1 durch alle Zahlen und schaue jeweils, ob ein Rest (d.h. eine Zahl ungleich 0) bei der Division entsteht. Wenn das immer der Fall ist, dann handelt es sich um eine Primzahl.
Dieses Verfahren lässt sich als Algorithmus formulieren, z.B. so:
ALGORITHMUS istPrimzahl:
Übergabe: n # natürliche Zahl
prim = True
k = 2
SOLANGE k < n:
WENN n % k == 0:
prim = False
k = k+1
Rückgabe: prim
Aufgabe 2
(a) Beschreibe den Verarbeitungsablauf mit einem Flussdiagramm. Informiere dich ggf. auf in den Abschnitten Fachkonzept - Wiederholung und Fachkonzept - Fallunterscheidung wie das geht.
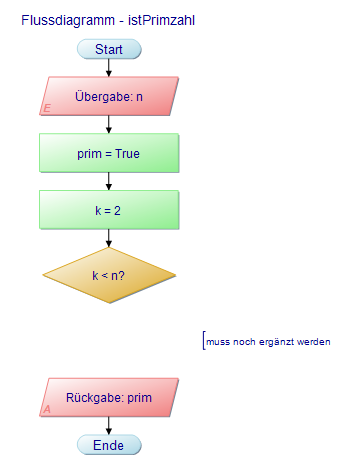
(b) Welche Rolle spielt die Variable prim im gezeigten Algorithmus?
Erkläre anhand eines Beispiels.
Aufgabe 3
(a) Warum reicht es, wenn man bei dem oben beschriebenen Verfahren n der Reihe nach durch alle Zahlen von 2 bis √n teilt?
(b) Hier ein zugehöriger Algorithmus. Erläutere anhand von Beispielen, wie der Algorithmus den Primzahltest durchführt.
ALGORITHMUS istPrimzahl:
Übergabe: n # natürliche Zahl
prim = True
k = 2
SOLANGE k*k <= n:
WENN n % k == 0:
prim = False
k = k+1
Rückgabe: prim
Aufgabe 4
Hier gibt es eine weitere Verbesserung des Algorithmus. Beschreibe die Verbesserung anhand eines Beispiels.
ALGORITHMUS istPrimzahl:
Übergabe: n # natürliche Zahl
prim = True
k = 2
SOLANGE k*k <= n und prim == True:
WENN n % k == 0:
prim = False
k = k+1
Rückgabe: prim
Aufgabe 5
Gibt es weitere Verbesserungsmöglichkeiten? Beschreibe sie in Worten oder baue sie in den Algorithmus ein.

