Fachkonzept - Funktion
Funktion als Verarbeitungseinheit
Funktionen kennst du aus der Mathematik.
Beispiel 1:
Die Funktion f mit der Funktionsdefinition f(x) = x2
ordnet jeder Zahl (aus einer noch festzulegenden Definitionsmenge) ihr Quadrat zu.
Der Funktionsaufruf f(3) liefert dann das Quadrat der Zahl 3 - also den Funktionswert 9.
Beispiel 2:
Die Funktionen A bzw. u mit den Funktionsdefinitionen
A(a, b) = a*b und u(a, b) = 2*a+2*b ordnen den Seitenlängen eines Rechtecks
den Flächeninhalt bzw. den Umfang des Rechtecks zu.
A(2, 5) liefert den Flächeninhalt 10 eines Rechtecks mit den Seitenlängen 2 und 5,
der Funktionsaufruf u(2, 5) den Umfang 14.
Funktionen werden nicht nur in der Mathematik benutzt, sie bilden auch ein wichtiges Werkzeug in der Informatik bei der automatisierten Datenverarbeitung.
Beispiel 3:
Die in Python vordefinierte Funktion ord liefert bei der Übergabe eines Zeichens die ASCII-Codezahl zurück.
Beispiel 4:
Umgekehrt liefert die in Python vordefinierte Funktion chr bei der Übergabe einer ASCII-Codezahl das entsprechende Zeichen zurück.
Ganz allgemein gilt:
Eine Funktion ist eine Verarbeitungseinheit, die übergebene Daten verarbeitet und den berechneten Funktionswert als Ergebnis zurückgibt.
Funktionsmodellierung
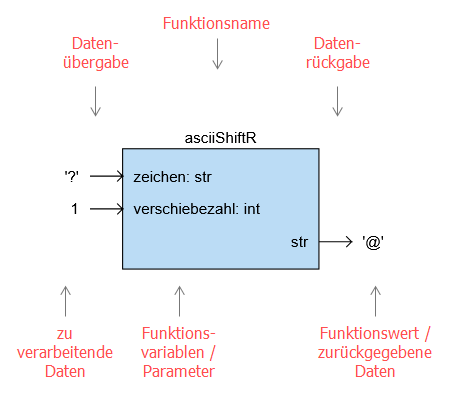
Als Beispiel betrachten wir eine Funktion, die eine Zeichenverschiebung im ASCII-Code bewirken soll.
Das Verhalten der Funktion lässt sich gut mit einem Black-Box-Diagramm verdeutlichen.
Wenn man der Verarbeitungseinheit ein Zeichen (aus der ASCII-Tabelle) und eine Verschiebezahl (aus dem Bereich 0..127) übergibt, dann berechnet sie ein neues Zeichen und gibt es zurück. Das neue Zeichen erhält man, indem man in der ASCII-Tabelle vom übergebenen Zeichen so viele Schritte weiter vorwärts läuft, wie die übergebene Verschiebezahl angibt.
Folgende Begriffe benutzt man bei der Funktionsmodellierung.
-
Eine Funktion hat einen Funktionsnamen.
Im Beispiel hat die Funktion den Namen
asciiShiftR. Den Funktionsnamen sollte man so wählen, dass das berechnete Ergebnis damit möglichst gut beschrieben wird. -
Zu verarbeitende Daten werden an Funktionsvariablen
(man sagt auch Parameter) übergeben.
Im Beispiel werden die beiden Parameter
zeichenundverschiebezahlbenutzt. - Eine Funktion gibt das Verarbeitungsergebnis als Funktionswert zurück.
Funktionsdefinition
Die Verarbeitung der übergebenen Daten erfolgt mit einer Funktionsdefinition. Diese Funktionsdefinition legt fest, wie die übergebenen Daten verarbeitet werden und aus ihnen der Funktionswert berechnet wird.
Im Fall der Funktion asciiShiftR könnte die Funktionsdefinition wie folgt aussehen:
# Funktionsdefinition
def asciiShiftR(zeichen, verschiebezahl):
zahl = ord(zeichen)
neueZahl = zahl + verschiebezahl
if neueZahl > 127:
neueZahl = neueZahl - 128
neuesZeichen = chr(neueZahl)
return neuesZeichen
Eine Funktionsdefinition besteht aus zwei Teilen, einem Funktionskopf und einem Funktionskörper.
Der Funktionskopf beginnt mit dem Schlüsselwort def. Es folgt der Funktionsname und in Klammern die
Auflistung der Parameter. Den Abschluss bildet der Doppelpunkt.
Der Funktionsrumpf dient zur Berechnung des Funktionswerts.
Mit einer return-Anweisung wird der zurückzuliefernde Funktionswert festgelegt.
Beachte, dass die Berechnungen selbst - wie das in Python üblich ist - eingerückt werden.
Funktionsaufruf
Mit einem Funktionsaufruf wird die Verarbeitungseinheit dann aktiviert, so dass sie für übergebene Daten jeweils eine Rückgabe erzeugt. In Python kann eine solche Aktivierung direkt im Ausführfenster erfolgen (sofern vorher das Programm mit der Funktionsdefinition einmal ausgeführt wurde, so dass Python die Funktionsdefinition kennt):
>>> asciiShiftR('?', 1)
'@'
>>> asciiShiftR('A', 3)
'D'
Ein Funktionsaufruf kann auch in einem Programm (oder in einer anderen Funktionsdefinition) erfolgen. Voraussetzung ist, dass die Funktion vorab definiert wurde.
# Funktionsdefinition
def asciiShiftR(zeichen, verschiebezahl):
...
# Funktionsaufrufe
print(asciiShiftR('?', 1))
print(asciiShiftR('A', 3))

