Goldbachs Vermutung
Summe von Primzahlen
Im Jahr 1742 teilte der Mathematiker Christian Goldbach seinem Kollegen Leonhard Euler eine interessante Beobachtung mit:
Jede gerade Zahl, die größer als 2 ist, lässt sich als Summe von zwei Primzahlen darstellen.
Hier der Brief, in dem die Beobachtung formuliert sein soll:
Viele Mathematiker haben seither versucht, Goldbachs Vermutung zu beweisen. Gelungen ist es bisher keinem.
Wir werden hier eine Funktion zur Überprüfung der Vermutung für einzelne Zahlen entwickeln.
Entwicklung einer Anzahlfunktion
Ziel ist es, eine Funktion zu entwickeln, mit der man die Anzahl der Zerlegungen einer geraden Zahl als Summe von zwei Primzahlen ermitteln kann.
Die Zahl 10 lässt sich als Summe 3+7 und 5+5 darstellen. Es gibt also 2 Zerlegungen als Summe von zwei Primzahlen.
Aufgabe 1
(a) Benutze die Funktion istPrimzahl als Baustein, um eine Funktionsdefinition für die Funktion anzahlzerlegungen
zu entwickeln.
from primzahltest import istPrimzahl
def anzahlZerlegungen(n):
"""
Verhalten:
Übergabe: gerade natürliche Zahl n größer als 2
Rückgabe: Anzahl der Kombinationen,
n als Summe von 2 Primzahlen darzustellen
Testfälle:
>>> anzahlZerlegungen(6)
1
>>> anzahlZerlegungen(10)
2
>>> anzahlZerlegungen(100)
6
"""
...
if __name__ == "__main__":
from doctest import testmod
testmod(verbose=True)
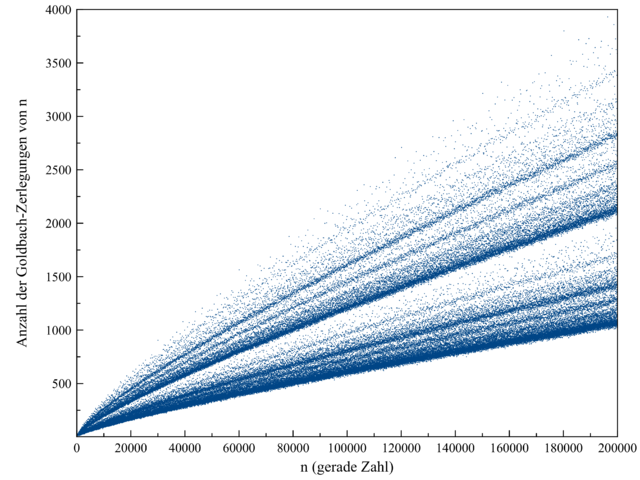
(b) Bestimme mit der entwickelten Funktion weitere Anzahlen und beobachte, wie diese Anzahlen mit wachsendem n ebenfalls wachsen. Vergleiche auch mit den Ergebnissen in der folgenden Abbildung.
(c) Was müsste die Funktion anzahlZerlegungen als Ergebnis liefern, wenn Goldbachs Vermutung nicht stimmen würde?
Quellen
- [1]: Brief von Goldbach an Euler - Urheber: Christian Goldbach - Lizenz: Gemeinfrei
- [2]: Goldbach-Zerlegungen - Urheber: Gadulu - Lizenz: Creative Commons BY-SA 3.0