Übungen
Aufgabe 1: Funktion als Baustein verwenden
Gegeben ist die Funktion primzahl mit folgender Funktionsdefinition:
def primzahl(n):
prim = True
if n == 1:
prim = False
else:
i = 2
while i <= n-1:
if n % i == 0:
prim = False
i = i+1
return prim
(a) Teste diese Funktion und erstelle eine Schnittstellenbeschreibung.
(b) Benutze die Funktion primzahl als Baustein, um eines der folgenden Probleme zu lösen:
(b1) Zu einer vorgegebenen natürlichen Zahl a soll die nächst größere Primzahl bestimmt werden.
(b2) Zu zwei vorgegebenen natürlichen Zahlen a und b sollen alle Primzahlen bestimmt werden, die zwischen diesen Zahlen liegen.
(b3) Zu einer vorgegebenen natürlichen Zahl a soll eine Primfaktorzerlegung bestimmt werden.
(c) Hier ein weiterer Baustein zum Primzahltest:
def primzahl(n):
prim = True
if n == 1:
prim = False
else:
i = 2
while i*i <= n:
if n % i == 0:
prim = False
i = i+1
return prim
Worin unterscheidet sich dieser Baustein vom oben gezeigte? Ersetze in einem Programm aus Teilaufgabe (b) den Baustein zum Primzahltest durch den neuen Baustein. Ändert sich hierdurch etwas am Verhalten des Programms?
Aufgabe 2: Schnittstellen beschreiben, Funktionen als Bausteine verwenden
(a) Gegeben ist die Funktion ggt mit folgender Funktionsdefinition:
def ggt(x, y):
while y > 0:
h = x % y
x = y
y = h
return x
Teste diese Funktion und erstelle eine Schnittstellenbeschreibung.
(b) Die Funktion addiereBrueche soll dazu dienen, Brüche zu addieren:
def addiereBrueche(bruch1, bruch2):
(zaehler1, nenner1) = bruch1
(zaehler2, nenner2) = bruch2
nennerSumme = nenner1 * nenner2
zaehlerSumme = zaehler1*nenner2 + zaehler2*nenner1
bruchSumme = (zaehlerSumme, nennerSumme)
return bruchSumme
Wenn man sie testet, erhält man ungekürzte Ergebnisse:
>>> addiereBrueche((1,4), (1,4))
(8, 16)
Benutze die Funktion ggt zur Verbesserung der Implementierung der Funktion addiereBrueche.
Fertige anschließend eine Schnittstellenbeschreibung für die Funktion addiereBrueche an.
Diese soll so gestaltet werden, dass man die Funktion benutzen kann, ohne dass man die Details
der Implementierung kennt.
(c) Entwickle und dokumentiere analog Funktionen zur Subtraktion, Multiplikation und Division von Brüchen.
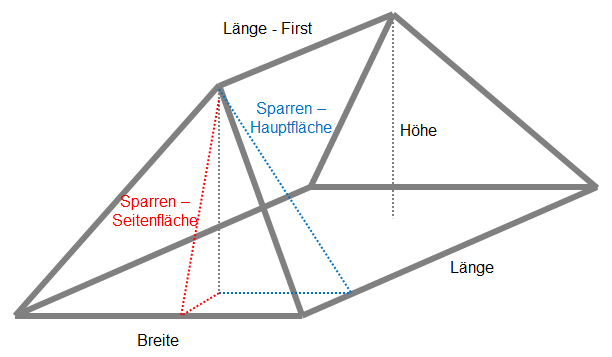
Aufgabe 3: Walmdach-Rechner
Die Abbildung zeigt, wie ein Walmdach aussieht. Man kann erahnen, dass die Berechnung der Fläche nicht ganz einfach ist. Bei einem Dachdecker-Betrieb gehört die komplexe Rechnung jedoch zum Tagesgeschäft und ein geeignetes Computerprogramm könnte hier möglicherweise sehr hilfreich sein.
Den Ziegelbedarf für ein Walmdach kann man mit einer Funktion abschätzen, die bei Übergabe der Größen des Dachs den gesamten Flächeninhalt des Dachs zurückliefert.
Die Größe eines Walmdachs lässt sich mit Länge, Breite, Höhe und der Länge des Dachfirsts beschreiben.
Entwickle eine Funktion zur automatisierten Berechnung der gesamten Dachfläche eines Walmdachs. Zerlege das Problem und benutze geeignete Hilfsfunktionen.
Aufgabe 4: für Experten
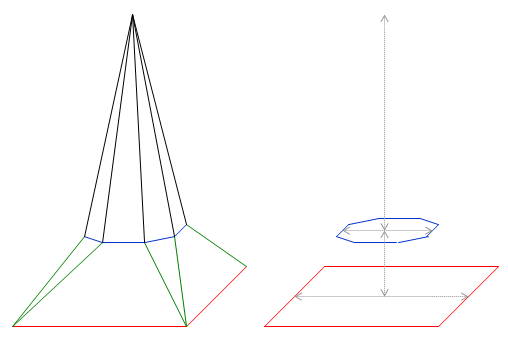
Viele Kirchtürme haben ein Dach, das so aussieht wie auf den Fotos:
Manchmal muss ein solches Dach auch neu eingedeckt werden. Dachdecker sollten in der Lage sein, den Materialbedarf für ein solches Dach zu berechnen.
Die folgende Abbildung zeigt die Dachstruktur dieser Kirchturmdächer.
Ziel ist es, einen flexiblen Flächenberechner für solche Kirchturmdächer zu entwickeln.
(a) Überlege zunächst, welche Dachgrößen man als Daten an eine geeignete Funktion übergeben möchte. Beschreibe das Verhalten der Funktion mit einem Black-Box-Diagramm.
(b) Führe die Flächenberechnungen für konkrete Dachmaße erst einmal direkt (ohne Funktionen) durch.
(c) Konzipiere geeignete Hilfsfunktionen.
(d) Erstelle eine Funktion zur Berechnung der Gesamtfläche eines Kirchturmdachs. Teste die Funktionsdefinition.
Aufgabe 5: eine komplexere Aufgabe für Mathematiker
Flächeninhalte unter Funktionsgraphen werden mit Hilfe von Unter- und Obersummen angenähert.
Entwickle geeignete Funktionen als Bausteine zur Bestimmung von Unter- und Obersummen zur Funktion f mit f(x)=x2. Frei wählbar soll das Intervall und die Anzahl der Unterteilungen sein. Am besten, du benutzt mehrere Funktionen zur Lösung der Teilprobleme.
Quellen
- [1]: Walmdach - Urheber: Shannon - Lizenz: Creative Commons BY-SA 3.0
- [2]: Größe eines Walmdachs - Urheber: KB - Lizenz: inf-schule.de
- [3]: Kirchturmdach 1 - Urheber: KB - Lizenz: inf-schule.de
- [4]: Kirchturmdach 2 - Urheber: KB - Lizenz: inf-schule.de
- [5]: Kirchturm mit Baugerüst - Urheber: KB - Lizenz: inf-schule.de
- [6]: Struktur eines Kirchturmdachs - Urheber: KB - Lizenz: inf-schule.de